Главная
ОЛИМПИАДНЫЕ ЗАДАЧИ ПО
ТЕОРИИ МАШИН И МЕХАНИЗМОВ
Олимпиады по теории машин и механизмов, проводимые в технических
вузах, а в последнее время и в классических университетах, являются
системообразующим элементом организации творческой учебно-познавательной
деятельности в высшей школе. Участие студентов в олимпиадном движении
способствует более упорядоченному и глубокому усвоению профессиональных знаний,
дает возможность сформировать у них готовность к творческой деятельности,
развить креативный характер мышления. Все это способствует подготовке
конкурентоспособного специалиста, готового к профессиональной деятельности в
современных рыночных условиях.
Задача 1 (2 балла)
Произвести классификацию четырех кинематических пар,
изображенных на рис.1, по трем признакам. Начертить оси и показать
относительные движения.
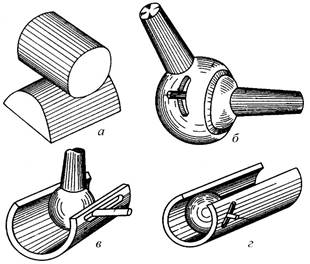
Рис.1
Решение.
Направления относительных движений.
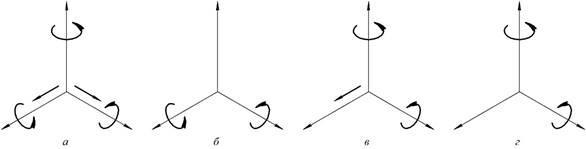
Классификация по трем признакам
|
Обозначение пары |
По характеру относительного движения |
По характеру соприкосновения элементов звеньев |
Число условий связи S |
|
а |
пространственная |
высшая |
1 |
|
б |
пространственная |
низшая |
4 |
|
в |
пространственная |
высшая |
3 |
|
г |
пространственная |
высшая |
4 |
|
Примечание: число условий
связи |
|||
Задача 2 (4,5 балла)
На рис.2 изображена структурная схема подъемного
механизма культиватора. Ведущим звеном является зубчатое колесо с внешними
зубьями. Колеса нарезаны без смещения исходного контура.
Необходимо:
1. Произвести структурный анализ механизма и
определить его степень подвижности (2 балла).
2. Начертить группы Ассура в
соответствии с порядком их присоединения к ведущему звену и написать формулу
строения механизма (2 балла).
3. Определить класс механизма (0,5 балла).
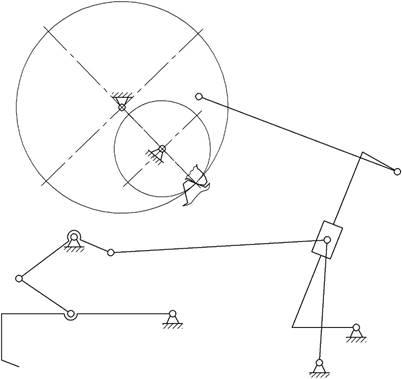
Рис.2
Решение.
1. Заменяем высшую (зубчатую) кинематическую пару
двумя низшими А и В (рис.2).
Степень подвижности механизма W определим по формуле Чебышёва П.Л.:
![]() ,
,
где n – число
подвижных звеньев; ![]() – число кинематических пар V класса;
– число кинематических пар V класса; ![]() – число
кинематических пар IV класса.
– число
кинематических пар IV класса.
Тогда ![]() до замены
высшей пары на низшие или
до замены
высшей пары на низшие или ![]() –
после замены.
–
после замены.
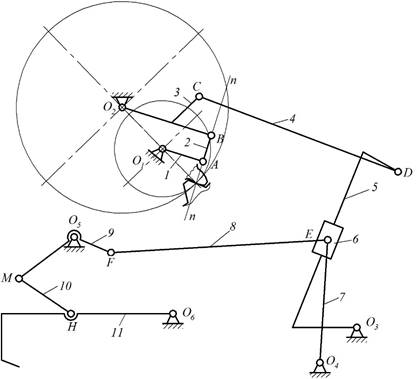
Рис.3
2. Группы Ассура и формула
строения механизма (рис.4)
![]()
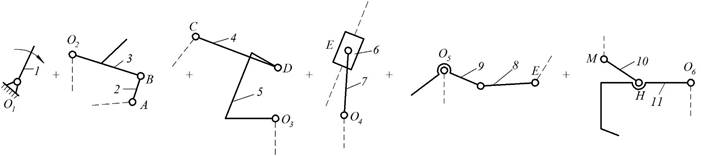
Рис.4
3. Класс механизма 2.
Задача 3 (6,5 баллов)
На фотографии (рис.5) изображен механизм открывания и
закрывания оконной рамы.
1. Изобразите структурную схему механизма (3 балла).
2. Определите степень подвижности механизма (1 балл).
3. Найдите группы Ассура,
определить их класс, запишите формулу строения механизма (2 балла).
4. Определите класс механизма (0,5 балла).

Рис.5
Решение.
1. Структурная схема механизма открывания оконной рамы
(рис.6).
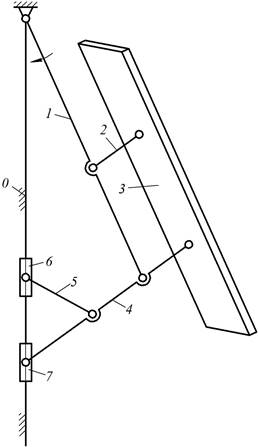
Рис.6
2. Степень подвижности механизма W определим по формуле Чебышёва П.Л.:
![]() ,
,
где n = 7 – число подвижных звеньев; ![]() – число кинематических пар V класса;
– число кинематических пар V класса; ![]() – число
кинематических пар IV класса.
– число
кинематических пар IV класса.
Тогда ![]() .
.
3. Формула строения механизма (рис.7).
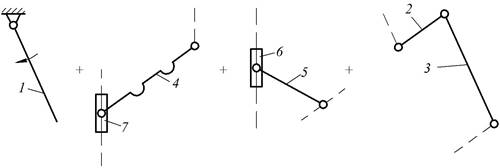
Рис.7
![]()
4. Механизм 2 класса.
Задача 4 (5
баллов)
В кулачковом механизме, изображенном на рис.8,
скорость толкателя в указанном положении ![]() при угловой
скорости кулачка
при угловой
скорости кулачка ![]() . Известны также эксцентриситет
. Известны также эксцентриситет ![]() и положение
толкателя
и положение
толкателя ![]() .
.
Необходимо:
1. Вычислить в текущем положении кулачкового механизма
значение угла давления и проверить на чертеже (4 балла).
2. Найти полюс зацепления, т.е. точку на кулачке, в
которой скорость по величине и направлению равна скорости толкателя. Изобразить
полюс на схеме механизма (1 балл).
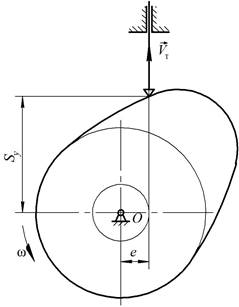
Рис.8
Решение.
1. Строим схему механизма и план скоростей в масштабах
(рис.9)
Скорость толкателя
![]() .
.
Направление вектора ![]() совпадает с
направлением касательной к профилю кулачка.
совпадает с
направлением касательной к профилю кулачка.
Расстояние
![]()
Скорость точки контакта на кулачке
![]()
![]()
Определим угол ![]() .
.
![]()
Угол давления ![]() определим из
следующих геометрических построений: проведем перпендикуляр к вектору
относительной скорости и получим направление нормали к профилю кулачка в точке
контакта.
определим из
следующих геометрических построений: проведем перпендикуляр к вектору
относительной скорости и получим направление нормали к профилю кулачка в точке
контакта.
![]()
![]()
![]()
![]()
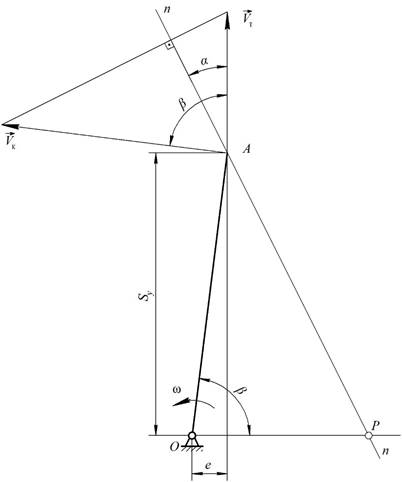
Рис.9
2. Определение положения полюса.
![]()
![]() .
.
Задача 5 (8,5 баллов)
Для механизма шарнирного четырехзвенника
построен план скоростей, имеющий вид равностороннего треугольника (рис.10).
Известно, что длины кривошипа ОА,
шатуна АВ и коромысла ВС находятся в соотношении ![]() . Скорость точки А
кривошипа
. Скорость точки А
кривошипа ![]() , угловая скорость кривошипа
, угловая скорость кривошипа ![]() .
.
Необходимо:
1. Построить в масштабе возможные варианты схемы
механизма с соответствующим планом скоростей (3 балла).
2. Найти длину стойки ОС – ![]() (1
балл).
(1
балл).
3. Определить в одном из вариантов угловую скорость коромысла
(0,5 балла).
4. Определить, который из построенных механизмов
является двухкривошипным или двухкоромысловым
или кривошипно-коромысловым (4 балла).
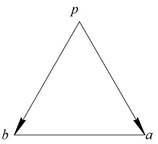
Рис.10
Решение.
1. Заданный план скоростей могут иметь четыре
механизма, схемы которых выполнены в масштабе на рис.11.
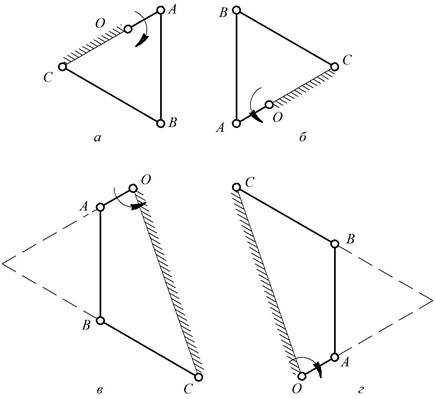
Рис.11. Схемы механизмов
2. Для механизмов а
и б очевидно, что длина стойки ![]() , а для механизмов в
и г длину стойки определим по теореме
косинусов,
, а для механизмов в
и г длину стойки определим по теореме
косинусов,
![]()
3. Угловая скорость коромысла у всех изображенных
механизмов в три раза меньше угловой скорость кривошипа ввиду того, что длина
коромысла в три раза больше длины кривошипа при одинаковой скорости точек А и В.
4. Варианты механизмов (рис.12, рис.13).
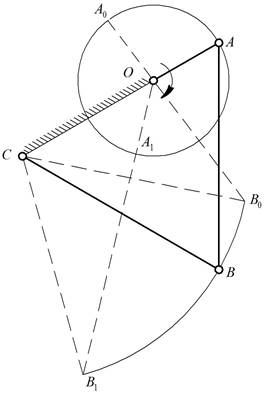
Рис.12. Схема кривошипно-коромыслового механизма
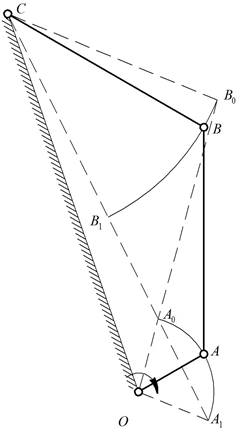
Рис.13. Схема двухкоромыслового
механизма
Задача 6 (4 балла)
Можно ли нарезать зубчатое колесо с модулем ![]() и числом зубьев
и числом зубьев
![]() без подреза с
помощью стандартной инструментальной рейки так, чтобы толщина зуба по
окружности вершин была не менее допускаемого значения
без подреза с
помощью стандартной инструментальной рейки так, чтобы толщина зуба по
окружности вершин была не менее допускаемого значения![]() .
.
Решение.
Толщина зуба на вершине
![]()
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Подставляя исходные данные, получим:
![]()
примем ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Расчетная толщина зуба по окружности вершин больше
допускаемой, следовательно, без подреза колесо нарезать можно.
Задача 7 (8 баллов)
У цилиндрической планетарной передачи с двумя внешними
зубчатыми парами передаточное отношение от водила Н к ведомому колесу 4 ![]() , а число зубьев ведомого колеса
, а число зубьев ведомого колеса ![]() . Все колеса имеют одинаковый модуль и нарезаны
стандартным реечным инструментом (рис.14).
. Все колеса имеют одинаковый модуль и нарезаны
стандартным реечным инструментом (рис.14).
1. Подобрать числа зубьев остальных колес (6 баллов).
2. Определить углы зацепления каждой пары колес (2
балла).
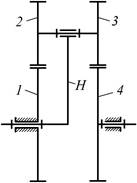
Рис.14
Решение.
1. Передаточное отношение планетарной передачи от
водила Н к ведомому колесу 4
![]()
Чтобы обеспечить заданное передаточное отношение,
принимаем ![]()
![]()
![]()
Тогда
![]()
2. Межосевые расстояния для колес, нарезанных без
смещения инструментальной рейки (нулевые зубчатые пары):
для первой пары колес
![]()
для второй пары колес
![]()
Межосевые расстояния должны быть равны, следовательно,
какую-то зубчатую пару необходимо нарезать со смещением.
Первый
случай. Если принять, что колеса 1 и 2
нарезаны без смещения (нулевая зубчатая передача), то ![]()
![]()
Тогда, чтобы получить ![]() вторая зубчатая
пара должна быть нарезана
с суммарным отрицательным смещением.
вторая зубчатая
пара должна быть нарезана
с суммарным отрицательным смещением.
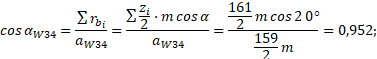
![]() и
и ![]()
Второй
случай. Если колеса 3
и 4 нарезаны без смещения, то ![]()
![]()
Тогда, чтобы получить ![]() первая зубчатая
пара должна быть нарезана с суммарным положительным смещением.
первая зубчатая
пара должна быть нарезана с суммарным положительным смещением.
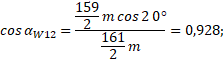
![]() и
и ![]()
Задача 8 (2,5 балла)
На рис.15 показан вид сверху на автомобильный
дифференциал заднеприводного автомобиля. Числа зубьев колес 3 и 5
равны. Сателлит 4 вращается вокруг
оси, закрепленной на водиле Н. Водило приводится во вращение парой конических колес 1 и 2.
Ведущие колеса машины ![]() и
и ![]() сидят на
полуосях зубчатых колес 3 и 5. Направление движения автомобиля
указано на рисунке.
сидят на
полуосях зубчатых колес 3 и 5. Направление движения автомобиля
указано на рисунке.
Частота вращения водила ![]() , а колеса 3
–
, а колеса 3
– ![]() .
.
Определить:
1. Частоту вращения колеса 5 – ![]() (2 балла).
(2 балла).
2. Движется ли машина прямо либо поворачивает направо
или налево (0,5 балла).
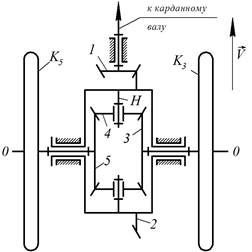
Рис.15
Решение.
1. Формула Виллиса для автомобильного дифференциала
![]()
Передаточное отношение зубчатого ряда
![]()
Подставляем (2) в (1),
![]()
откуда
![]()
При ![]()
![]() , т.е. при остановившемся водиле колеса вращаются в
разные стороны.
, т.е. при остановившемся водиле колеса вращаются в
разные стороны.
Подставляя исходные данные в (1) и учитывая (2),
получаем:
![]()
![]()
![]()
2. Скорость вращения левого колеса ![]() больше скорости
вращения правого колеса
больше скорости
вращения правого колеса ![]() , следовательно, машина поворачивает
направо.
, следовательно, машина поворачивает
направо.
Задача 9 (9,5 баллов)
Воздушный компрессор приводится во вращение
двигателем, вал которого имеет среднюю частоту вращения ![]() . Создаваемый двигателем момент
. Создаваемый двигателем момент ![]() и момент
сопротивления со стороны компрессора
и момент
сопротивления со стороны компрессора ![]() зависят от
углового положения вала двигателя, и равны, соответственно,
зависят от
углового положения вала двигателя, и равны, соответственно,
![]()
![]()
![]()
![]()
Для уменьшения вибрации угловой скорости между
двигателем и компрессором помещен маховик с моментом инерции ![]() относительно
оси вращения. Инертностью других вращающихся частей машинного агрегата можно
пренебречь.
относительно
оси вращения. Инертностью других вращающихся частей машинного агрегата можно
пренебречь.
Определить:
1. Коэффициент неравномерности вращения вала двигателя
(9 баллов).
2. Среднюю мощность двигателя (0,5 балла).
Решение.
1. Построим графики движущего момента и момента
сопротивления в зависимости от угла поворота вала двигателя (рис.16).
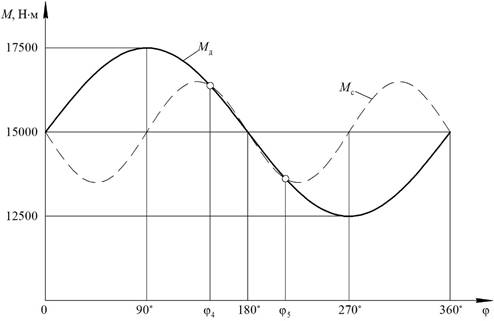
Рис. 16. Графики моментов
Рассматривая графики, а также зависимости моментов от
угла поворота, определяем, что движущий момент равен моменту сопротивления при
углах ![]() ,
, ![]() ,
, ![]() . Два других угла определим аналитически.
. Два других угла определим аналитически.
![]()
Заменив ![]() , получим в итоге
, получим в итоге ![]() .
.
![]() ;
; ![]()
Запишем дифференциальное уравнение движения механизма
![]()
Учитывая, что ![]() ,
,
![]()
Следовательно, экстремальные (максимальные и
минимальные) значения угловой скорости соответствуют рассмотренному выше
условию равенства моментов.
Качественный график изменения угловой скорости вала
двигателя приведен на следующем рисунке 17.
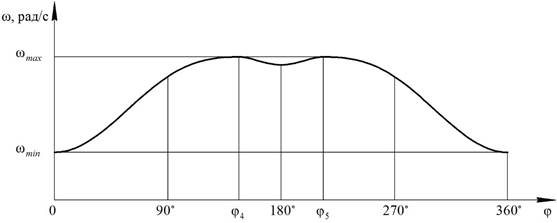
Рис. 17. График угловой скорости вала двигателя
Из рис.16 очевидно, что ![]() соответствует
соответствует ![]() , а
, а ![]() –
– ![]() . В этих пределах проинтегрируем дифференциальное
уравнение движения механизма.
. В этих пределах проинтегрируем дифференциальное
уравнение движения механизма.
![]()
![]()
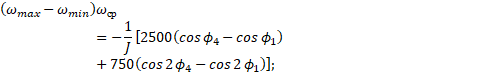
![]()
![]()
Согласно условиям задачи средняя угловая скорость
![]()
Тогда
![]()
Коэффициент неравномерности
![]()
2. Средняя мощность на валу двигателя
![]()
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Строительная механика