Лабораторные работы

Главная

Лабораторная работа №7

Построение кинематических схем плоских и пространственных механизмов

Цель работы: построение кинематических схем и определение степени подвижности механизма.

Объект исследования: модели механизмов.

Звеньями называют образующие механизм твердые тела, точки которых не могут иметь относительных перемещений.

Кинематической парой (сокращенно – парой) называют подвижное соединение соприкасающихся звеньев.

Элементы пары – совокупность поверхностей линий и точек контакта звеньев.

Кинематические пары классифицируются по числу Н степеней свободы в относительном движении звеньев или по числу S условий связи (ограничений), накладываемых на относительное движение (табл.1), высшие пары обеспечивают контакт двух звеньев по линии или в точке, низшие – по поверхности.

Изображение кинематических пар	Подвижность	Число степеней свободы	Число условий связи	Класс пары
1	2	3	4	5
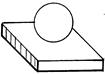
Шар-плоскость	Пятиподвижная	5	1	1
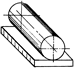
Цилиндр-плоскость	Четырёхподвижная	4	2	2
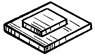
Плоскостная Сферическая	Трехподвижная	3	3	3
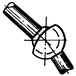
Цилиндрическая Сферическая с пальцем	Двухподвижная	2	4	4
Вращательная Поступательная Винтовая	Одноподвижная	1	5	5

Кинематическая цепь – система звеньев, образующих между собой кинематические пары. В замкнутой цепи каждое звено входит не менее, чем в две кинематические пары, и совокупность ее звеньев и пар образует один (простая кинематическая цепь) или несколько замкнутых контуров (сложная кинематическая цепь). Необходимым признаком сложной кинематической цепи является наличие звена, входящего более, чем в две пары.

Механизм – кинематическая цепь, одно из звеньев которой неподвижно (стойка). Механизм служит для преобразования движений, сообщаемых входным звеньям, в требуемое движение выходного звена. Причем, число входных звеньев равно числу обобщенных координат, однозначно характеризующих положение звеньев кинематической цепи относительно стойки, т. е. числу степеней свободы механизма (W).

Число (K) независимых контуров в механизме определяется по формуле Гохмана:

, (1)

где – суммарное число кинематических пар;

n – число подвижных звеньев.

Контур считается независимым, если он не может быть образован сложением двух других контуров.

В зависимости от класса кинематической пары на относительное движение звеньев налагается определенное число условий связи. Число же степеней свободы кинематической цепи

Н = 6N – (5P₅ + 4Р₄ + 3Р₃ + 2P₂ + P₁).

где N – число звеньев кинематической цепи.

Если одно звено этой цепи стойка, тогда число степеней свободы всей цепи уменьшится на шесть, т.е. Н – 6 = W – число степеней свободы кинематической цепи относительно стойки.

Для преобразования движения входных звеньев, совершаемых в одной плоскости в движение выходного звена в той же плоскости достаточно использовать плоские кинематические цепи, все звенья которых перемещаются в одной (или параллельных) плоскостях, а на подвижность звеньев вне этой плоскости наложены 3 общих ограничения. При условии, что оси всех кинематических пар параллельны (идеально плоский механизм), число степеней свободы W плоских механизмов относительно стойки определяется по структурной формуле Чебышева:

, (2)

где: р₅ – число пар 5-го класса;

р₄ – число пар 4-го класса.

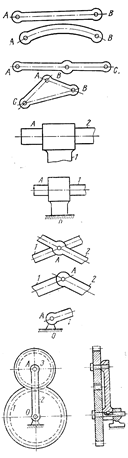
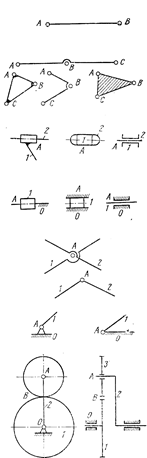
При структурном анализе механизмов пользуются их схематичным изображением. При этом структурная схема может вычерчиваться без соблюдения масштаба. Некоторые условные обозначения звеньев, плоских кинематических пар и механизмов представлены на рис. 1 и в табл. 2.

Рис. 1

Наименование	Конструктивное изображение	Схематичное изображение
Звено: Звено входит в две вращательные пары
звено входит в три вращательные пары
Поступательная пара: оба звена подвижные
одно звено неподвижно
Вращательная пара: оба звена подвижные
одно звено неподвижно
Дифференциальный зубчатый механизм

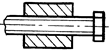
Избыточные связи в идеально плоском механизме возникают в результате использования в каждой кинематической паре большего, чем необходимо для геометрической связи, числа элементов – локальные избыточные связи (рис.2), а так же применение большего, чем необходимо для передачи движения, количества подвижных звеньев, т.е. дополнительных звеньев (рис. 3).

Рис. 2

Рис.3

Излишние (дополнительные) подвижности, не влияющие на подвижность выходного звена в кинематической цепи, могут иметь отдельные звенья (местная излишняя подвижность) механизма (рис. 4) или часть звеньев (групповая излишняя подвижность) механизма.