Главная

Лабораторная работа №21

Построение эвольвентных зубчатых профилей методом обкатки с помощью

учебных приборов, расчет и проектирование зубчатой передачи

Цель работы: изучить теоретические основы нарезания эвольвентных зубчатых колес рейкой методом обкатки и влияние смещения зубчатой рейки на форму нарезаемых колес, изучить методику расчета основных параметров зубчатых колес, изучить методику расчета и проектирования зубчатой передачи, с использованием блокирующего контура.

Получение эвольвентных профилей методом обкатки

Геометрическая форма и размеры зубьев нарезаемого колеса зависят от формы, размеров инструмента и его положения относительно заготовки колеса.

По методу обкатки зубья колес нарезаются (рис.1) долбяками на зубодолбежных станках, гребенками на зубострогальных станках, червячными фрезами на зубофрезерных станках.

Метод обкатки базируется на теории эвольвентного зацепления, основное положение которого заключается в том, что движущемуся инструменту и заготовке сообщаются относительные движения, одинаковые с движениями звеньев соответствующий зубчатой передачи.

Одним из преимуществом этого метода является то, что он позволяет одним и тем же инструментом нарезать зубчатые колеса с любым числом зубьев и различной формы профиля.

В процессе обкатки заготовки колеса инструментом происходит перекатывание без скольжения делительной окружности нарезаемого колеса по любой прямой исходного контура инструмента, параллельной его делительной прямой.

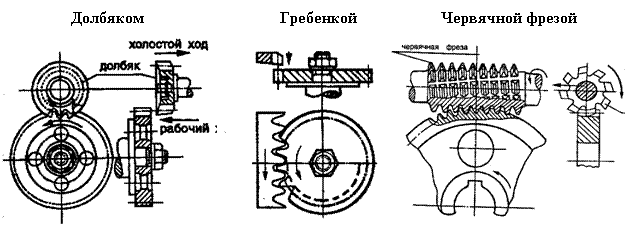
Рис.1

Делительной прямой инструмента является прямая, по которой толщина его зуба равна ширине впадины.

Положение инструмента относительно заготовки нарезаемого колеса определяется его смещением (xm) исходного производящего контура, за которое принято кратчайшее расстояние между делительнойной окружностью нарезаемого колеса и делительной прямой номинальной исходной производящей рейки (инструмента). Здесь x – коэффициент смещения инструмента – отношение смещения к модулю нарезаемого зубчатого колеса; m – расчетный модуль (или просто модуль) цилиндрического зубчатого колеса, равный делительному нормальному модулю, за который принята линейная величина в π раз меньшая нормального шага зубьев, являющегося кратчайшим расстоянием между одноименными профилями соседних зубьев, замеренным по делительной окружности колеса (размерность модуля в мм).

Можно нарезать три вида зубчатых колес методом обкатки (рис.2):

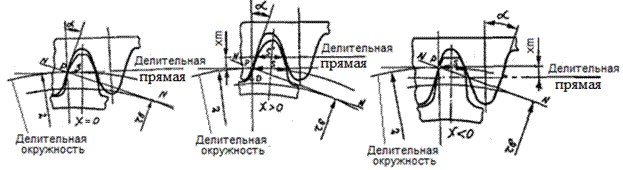
Рис.2

1) колеса без смещения (x=0), полученные при перекатывании делительной окружности нарезаемого колеса по делительной прямой исходного контура инструмента;

2) колеса с положительным смещением (центральная часть рис.2), полученные при обкатки делительной окружности по прямой, параллельной делительной прямой и отстоящей от нее на величину положительного смещения +xm (инструмент как бы удаляется от центра заготовки x>0);

3) колеса с отрицательным смещением (x<0), полученные аналогично, но при отрицательном смещении -xm (инструмент как бы приближается к центру заготовки).

Наименьшее расстояние между центром заготовки и делительной прямой исходного контура инструмента лимитируется отсутствием подрезания зубьев нарезаемого колеса. При подрезании часть эвольвентного профиля у основания зуба нарезаемого колеса срезается в результате интерференции зубьев при станочном зацеплении (рис.3).

Другой дефект зуба при станочном зацеплении, связанный с явлением интерференции, заключается в срезании зуба. Срезание зуба – это срезание части номинальной поверхности у вершины зуба обрабатываемого колеса в результате интерференции зубьев при станочном зацеплении.

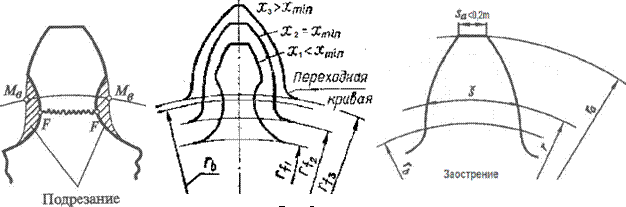
Рис.3

Минимальная величина коэффициента смещения x_min для реечного исходного контура, обеспечивающая отсутствие подрезания зуба, определяется по формуле:

где x_min – коэффициент наименьшего смещения исходного контура; h_a^* - коэффициент высоты головки зуба исходного контура инструмента; z_min – наименьшее число зубьев свободное от подрезания; z – число зубьев нарезаемого колеса

где - угол профиля зуба рейки.

Максимальная величина смещения исходного контура инструмента ограничивается заострением вершин зубьев нарезаемого колеса. Считается, что имеет место заострение если (рис.3), для тяжело нагруженных передач - .

Основные элементы зубчатой передачи

Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару.

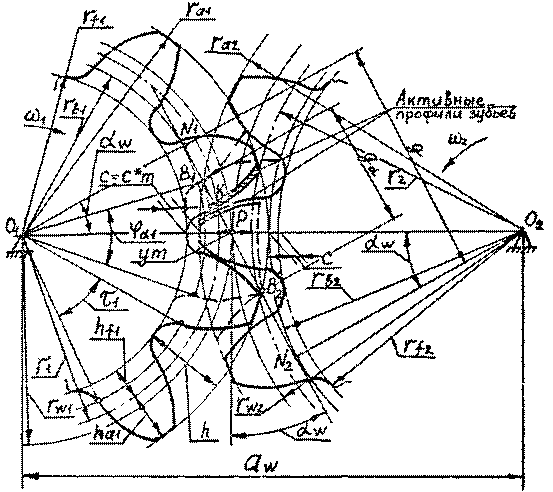
Рис.4

К основным параметрам, характеризующим зубчатую передачу (рис.4), относятся: межосевая линия, межосевое расстояние a_w , полюс зацепления, линия зацепления, угол зацепления , дуга зацепления.

Межосевая линия О₁О₂ – прямая линия, пересекающая оси зубчатых колес передачи под прямым углом.

Межосевое расстояние a_w - расстояние между осями зубчатых колес передачи по межосевой линии.

Линия зацепления N₁N₂ - траектория общей точки контакта зубьев при ее движении относительно неподвижного звена зубчатой передачи, которая при линейном контакте определяется в ее главном сечении. g – длина линии зацепления.

Полюс зацепления зубчатой передачи – точка касания начальных поверхностей зубчатых колес передачи. Определяется как точка пересечения межосевой линии и линии зацепления.

Активная линия зацепления В₁В₂ – часть линии зацепления зубчатой передачи, соответствующая активной действующей линии зуба или, при линейном контакте, активным профилям взаимодействующих зубьев в главном сечении зубчатой передачи, g_a - длина активной линии зацепления.

Длина дополюсной части активной линии зацепления g_f – длина части активной линии зацепления, соответствующая углу дополюсного перекрытия зубчатого колеса эвольвентной передачи.

Длина заполюсной части активной линии зацепления g_a – длина части активной линии зацепления, соответствующая углу заполюсного перекрытия зубчатого колеса эвольвентной передачи.

N₁, N₂, B₁, B₂ – предельные точки линий зацепления и ее активной части. Предельная точка линии зацепления – это каждая из точек, ограничивающих линию зацепления зубчатой передачи и соответствующих предельным точкам действующей теоретической поверхности зуба, которая при линейном контакте является точкой пересечения линии зацепления с предельной линией поверхности зацепления.

Угол зацепления – острый угол в главном сечении эвольвентной цилиндрической зубчатой передачи между линией зацепления и прямой, перпендикулярной к линии центров.

Рабочий профиль зуба – это профиль зуба, расположенный на его рабочей стороне. Рабочая сторона зуба – это боковая поверхность зуба, участвующая в передаче движения. Но в зацеплении участвует не весь эвольвентный, т.е. теоретический рабочий профиль, а только часть его, которая называется активным профилем. Активный профиль зуба – эта часть профиля зуба, соответствующая его активной поверхности. Активная поверхность - часть боковой поверхности зуба, по которой происходит взаимодействие с боковой поверхностью зуба парного зубчатого колеса (т.е. находящееся с ним в зацеплении). mn, ef – фактические рабочие профили зубьев, где m, f – верхние точки активного профиля. Верхняя точка активного профиля – это точка активного профиля, наиболее близкая к его вершине. n, e – нижние точки активного профиля. Нижняя точка активного профиля – это точка активного профиля, наиболее близкая к его переходной кривой.

Дугой зацепления cd называется расстояние между рабочим профилем зуба одного колеса, входящего в зацепление в т. В₁ и выходящего из него в т. В₂, измеренное по дуге окружности. Дуга зацепления может быть отмечена по любой окружности: начальной, делительной, основной.

Начальная окружность делит зубья на начальную головку и начальную ножку.

Высота начальной головки зуба h_wa – расстояние между окружностью вершин зубьев и начальной окружностью цилиндрического зубчатого колеса. Высота начальной ножки зуба колеса h_wf – расстояние между начальной окружностью и окружностью впадин цилиндрического зубчатого колеса. Высота зуба колеса h – расстояние между окружностями вершин и падин цилиндрического зубчатого колеса.

Радиальным зазором с называется расстояние между окружностью вершин одного колеса и окружностью впадин другого колеса:

где m – модуль в мм; – коэффициент радиального зазора.

Воспринимаемое смещение ym - разность межосевого расстояния цилиндрической зубчатой передачи со смещением и ее делительного межосевого расстояния

где а_wо – делительное межосевое расстояние, равное полусумме делительных диаметров зубчатых колес при внешнем зацеплении и полуразности при внутреннем зацеплении; y – коэффициент воспринимаемого смещения, равный отношению воспринимаемого смещения к расчетному модулю цилиндрического зубчатого колеса.

Иначе говоря, воспринимаемое смещение – это расстояние между делительными окружностями колес, измеренное по линии центров.

Коэффициентом перекрытия учитывает непрерывность и плавность работы зубчатого зацепления. Коэффициент перекрытия выражается отношением длины дуги зацепления (T_b, T_w, T) по какой – либо окружности (основной, начальной или делительной) к шагу (p_b, p_w, p) по той же окружности.

Если дуга зацепления меньше шага (), то зацепление будет прерывистым, с повторяющимися ударами в момент входа очередной пары зубьев в зацепление. При дуге зацепления равной шагу () зацепление можно считать непрерывным только теоретически. Нормально работающая передача должна иметь . Для зацепления с прямыми зубьями при и теоретическим пределом является значение

Краткие сведения о зубчатых передачах со смещением

Зубья передач со смещением изготавливают на тех же станках и тем же стандартным инструментом, что и зубья передач без смещения.

Разница заключается в том, что при изготовлении зубчатых колес со смещением инструмент устанавливают с некоторым смещением в радиальном направлении (рис.2 и рис.3). Соответственно, заготовки колес со смещением выполняют с измененным диаметром.

Смещение инструмента определяется по формуле:

где – коэффициент смещения; m – модуль изготавливаемого зубчатого колеса.

На рис.3 показаны зубья, изготавливаемые одним и тем же инструментом, но с различными коэффициентами смещения. Из рисунка видно, что чем больше значение коэффициента смещения, тем профиль зуба более далеко отстоит от основной окружности. При этом уменьшается кривизна эвольвентного профиля и зуб у основания утолщается, а у вершины заостряется.

При колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением z уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Если число зубьев z достигает некоторого предельного значения z_min, то при нарезании зубьев инструментом реечного типа происходит подрезание ножек зубьев. В результате этого значительно снижается прочность зуба на изгиб. По границе подрезания устанавливается минимально допустимое число зубьев. При нарезании прямых зубьев эвольвентного зацепления стандартным инструментом реечного типа минимально допустимое число зубьев, определенное по формуле (2), z_min=17.

Как выше отмечалось устранить подрез зубьев при z<z_min можно за счет положительного смещения при нарезании зубатых колес.

Необходимо также помнить, что при большом числе зубьев смещение малоэффективно, так как форма зуба при этом почти не изменяется (у рейки и смещение совершенно не изменяет форму зуба).

Смещение инструмента при нарезании цилиндрических зубчатых колес используется также для вписывания передачи в заданное межосевое расстояние.

Блокирующие контуры

Необдуманный выбор численных значений коэффициентов смещения при проектировании зубчатой передачи может привести к следующим дефектам зубьев колес и зубчатого зацепления.

1. Интерференции зубьев - явление, состоящее в том, что при рассмотрении теоретической картины зубчатого зацеления часть пространства оказывается одновременно занятой двумя взаимодействующими зубьями.

2. Уменьшению коэффициента перекрытия и переходу за предельное значение . Для прямозубых передач рекомендуется , для косозубых .

3. Заострению зубьев и переходу за предельное значение S_a=0, где S_a – толщина зубьев по окружности выступов. Наименьшая предельно допустимая толщина зуба по окружности выступов колес для тяжело нагруженных передач: при поверхностном упрочнении зубьев равна 0,4m; для колес с однородной структурой материала зубьев – 0,3m (рис.5).

4. Подрезанию зубьев (рис.5).

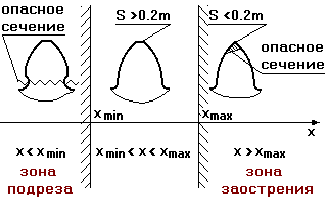
Рис.5

При проектировании зубчатой передачи составленной из колес с числами зубьев z₁ и z₂ и модулем m проектирование зубчатого зацепления сводится к выбору коэффициентов смещения х₁ и х₂ зубчатых колес.

Наиболее удобно рассматривать ограничения, накладываемые на х₁ и х₂, в системе координат, где по оси абсцисс откладываются значения коэффициента смещения х₁ а по оси ординат х₂ (рис.6). Предельным значениям каждого из перечисленных выше 4-х факторов в этой системе координат соответствует определенная линия, отделяющая зону допустимых значений х₁ и х₂ от зоны недопустимых.

Линии блокирующего контура (см. рис.6):

1 – линия коэффициента перекрытия (фиолетовая линия на рисунке, получаемом при работе с программой block);

2 – линия коэффициента перекрытия (фиолетовая линия на рисунке, получаемом при работе с программой block);

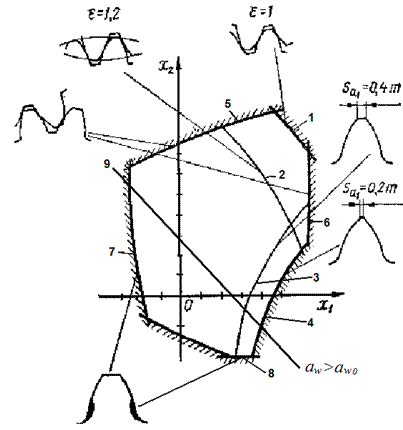
Рис.6. Блокирующий контур

3 – линия толщины зуба шестерни (шестерней называют колесо передачи, имеющее меньшее число зубьев) по окружности выступов (зеленые линии на рисунке, получаемом при работе с программой block);

4 – линия толщины зуба шестерни по окружности выступов ;

5 – граница интерференции на ножке зуба колеса (желтые линии на рисунке, получаемом при работе с программой block);

6 – граница интерференции на ножке зуба шестерни (желтые линии на рисунке, получаемом при работе с программой block);

7 – линии минимальной величины коэффициента смещения х₁ при изготовлении шестерни из условия отсутствия подреза зубьев (красная линия на рисунке, получаемом при работе с программой block);

8 – линии минимальной величины коэффициента смещения х₂ при изготовлении колеса из условия отсутствия подреза зубьев (красная линия на рисунке, получаемом при работе с программой block);

9 – изолиния заданного межосевого расстояния а_w (голубая линия на рисунке, получаемом при работе с программой block); при межосевом расстоянии, равном делительному а_wо, изолиния 9 проходит через начало системы координат.

Таким образом, блокирующий контур представляет собой область допустимых значений коэффициентов смещения х₁ и х₂, при которых обеспечивается благоприятные условия зацепления колес: отсутствие подрезания и интерференции, обеспечение требуемого коэффициента перекрытия, отсутствие заострения и т.д.

Зона внутри контура, выделенного на рис.6 штриховкой, определяет область допустимых значений х₁ и х₂, и является блокирующим контуром.

Оборудование

Прибор ТММ-42 для вычерчивания эвольвентных профилей методом обкатки, бумажный круг («заготовка») из ватмана, чертежный карандаш, циркуль, масштабная линейка, лист кальки (формат А4), программы ”Spurgear” и «Bloсk».

Чтобы изучить влияние смещения инструмента на форму профиля зуба и выявить условия, обеспечивающие отсутствие его подрезания, работу проводим на приборе ТММ-42, имитирующем метод обкатки. Общий вид прибора представлен на рис.7.

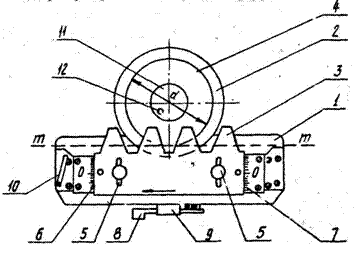
Рис.7

На основании 1 прибора установлены диск 2 и рейка 3, имитирующая инструмент для изготовления зубчатого колеса. Диск состоит из двух частей: верхней части 2, выполненной из органического стекла и представляющей собой круг с диаметром, равным диаметру заготовки колеса, и нижней части 4 – круга с диаметром, равным диаметру делительной окружности. Оба круга жестко соединены между собой и могут вращаться на оси, укрепленной в основании прибора. Рейка закреплена винтами 5. По бокам рейки размещены две шкалы 6 и 7, а на рейке имеются две риски (справа и слева), служащие для отсчета смещения xm (мм).

Если исходный контур инструмента располагается так, что его делительная прямая m – m касается делительной окружности заготовки, то на последней получим профили зубьев колеса без смещения. Риски на рейке 3 будут совпадать с нулевыми отметками шкал 6 и 7.

При смещении исходного контура инструмента относительно прямой m – m можно получить профили зубьев колес с положительным или отрицательным смещением. Перемещение рейки отсчитывается по шкалам 6 и 7, после чего она фиксируется винтами 5.

Прерывистое поступательное перемещение рейки осуществляется клавишей 8. При нажатии клавиши 8 рабочей собачкой храпового механизма рейка 3 подается влево (по стрелке) на 4 – 5 мм.

Рядом с клавишей 8 находится Г – образная рукоятка 9 свободного хода каретки. В правом положении (рукоятка лежит на упорном штифте) обеспечивается нормальная работа клавиши 8 (т.е. шаговое поступательное перемещение рейки); при повороте рукоятки против часовой стрелки каретка с рейкой перемещается свободно от руки вправо и влево.

Перемещение рейки 3 и поворот диска 2 согласуются при помощи натянутой струны. Чтобы повернуть диск для установки в определенное положение, струну нужно ослабить. Для этого рукоятку 10 прибора нужно повернуть против часовой стрелки. Для натяжения струны рукоятку 10 ставят в положение верхнего упора.

Порядок выполнения работы

Преподаватель указывает студенту номер зубчатой передачи (см. таблицу) для которой необходимо вычертить зубчатые колеса и провести расчет и проектирование зубчатого зацепления.

Таблица данных для лабораторной работы №3

№ Зубчатой передачи	Числа зубьев колес передачи				Модули зубчатых колес m, мм	aw, мм
	z1	№ прибора для получе-ния профи-лей зубьев	z2	№ прибора для получе-ния профилей зубьев
1	10	2	11	3	13	145
2	10	2	12	4	13	155
3*	11	3	11	3	13	155
4	11	3	12	4	13	160
5*	12	4	12	4	13	165
6	10	6	11	7	14	160
7*	11	7	11	7	14	163
8*	11	11	11	11	15	175
9	11	11	12	12	15	185
10*	12	12	12	12	15	188

В таблице * отмечены предпочтительные варианты передачи.

I этап. Вычерчивание эвольвентных профилей зубьев при нулевом смещении инструмента методом обкатки (огибания).

1. Ознакомиться с устройством прибора ТММ – 42 и его работой, опробовать механизм передвижения рейки.

2. В отчет по лабораторной работе записать номер прибора (прибор выбирается по таблице в зависимости от номера зубчатой передачи) и заданные величины: модуль (m), угол профиля рейки (), коэффициент высоты головки зуба (), диаметр делительной окружности (d).

3. Вычислить параметры колеса без смещения:

число зубьев колеса z=d/m;

диаметр основной окружности

шаг по делительной окружности

шаг по основной окружности

толщина зуба по делительной окружности

толщина зуба по основной окружности

где.

4. Отвинтив винт 12, снять крышку 11, за ней снять и бумажный круг, имитирующий заготовку колеса.

На заготовке провести циркулем делительную и основную окружности (центр заготовки отмечен проколом тонкой иглы). Установить заготовку на прежнее место.

Установить рейку, чтобы риски на рейке были против нулевых делений шкал.

5. Бумажный круг наложить на три иглы диска 2 и прижать крышкой 2, предварительно отвинченной винтом 12.

6. Поворотом рукоятки 9 против часовой стрелки освободить рейку от храпового механизма и перевести ее в крайнее правое положение. Затем обеспечить рабочее состояние рейки, повернув ту же рукоятку 9 до упорного штифта.

7. Обвести карандашом на бумажном круге контур профилей зубьев рейки.

8. Нажимом на клавишу 8 передвинуть рейку влево на один шаг и вновь обвести контур зубьев рейки. Так делается до тех пор, пока рейка не дойдет влево до упора и на бумажном круге получиться 2-3 хорошо вычерченных зуба колеса.

II. этап. Расчет и проектирование зубчатой передачи.

1. Определить по формуле (1) делительное межосевое расстояние заданной преподавателем зубчатой передачи .

Выбрать из ряда R_a40 нормальных линейных размеров численное значение начального межосевого расстояния а_w , причем а_w>а_wо и является ближайшим к нему.

2. Используя программу ”Spurgear” определить для заданного модуля какие пары чисел зубьев колес z₁ и z₂ возможны при выбранном начальном межосевом расстоянии а_w.

Убедиться, что колеса с заданными z₁ и z₂ среди них встречаются. В противном случае изменить межосевое расстояние. Если подобрать начальное межосевое расстояние не удается, то перейти к п.3, взяв значение а_w из таблицы №3.

3. Для заданного а_w, m, z₁ и z₂ с помощью программы «Block» построить блокирующий контур и определить коэффициенты смещения х₁ и х₂.

Если числа зубьев z₁ и z₂ одинаковы, то и коэффициенты смещения х₁ и х₂ также должны быть одинаковы.

Выбрать х₁ и х₂ с помощью полученного блокирующего контура.

Рассчитать с помощью программы «block» параметры зубчатых колес и зацепления и занести данные в отчет:

4. Вычертить эвольвентные профили зубьев с выбранным положительным смещением на учебном приборе ТММ – 42, имеющем, указанный в таблице данных номер.

5. Освободив винты 5, рейку отодвинуть от оси заготовки на величину рассчитанного смещения x₁m (мм), которое устанавливается по шкалам 6 и 7. Затем рейку вновь закрепить винтами 5.

6. Поворотом рукоятки 10 влево до отказа диск с бумажным кругом освободить и повернуть примерно на 120⁰ относительно неподвижной рейки. После этого рукоятку 10 вновь перевести в правое положение, связав общее движение диска 2 и рейки 3.

7. Методом, указанным в пп.7 – 8 (I-го этапа), вычертить три зуба колеса с положительным смещением.

8. Если числа зубьев колес передачи разные z₁ и z₂, то п. 5 - 7 выполняются и для второго колеса.

9. На изображение зубчатых колес нанести циркулем окружность вершин колеса с положительным смещением. Измерить толщину зуба по окружности вершин и сравнить полученные значения с расчетными.

10. Вычертить зубчатую передачу на карандашной кальке или листе бумаги формата А4 в масштабе 1:1 (рис.1).

11. Провести межосевую линию.

12. На межосевой линии отложить межосевое расстояние О₁О₂ (а_w), где О₁ – центр шестерни; О₂ – центр колеса.

13. Из центра О₁ провести окружности впадин и вершин шестерни (r_{f 1}, r_a1).

14. Из центра О₂ провести окружности впадин и вершин колеса (r_{f 2}, r_a2).

15. Из центров О₁ и О₂ провести основныеокружности колес (r_в1, r_в2).

16. Провести внутреннюю касательную к основным окружностям, отметив на ней точки касания N₁ и N₂ , определяющие линию зацепления длной q.

17. На межосевой линии отметить полюс запления П.

18. Под кальку подложить заготовку, совместить ее центр с центром О₁. Вокруг этого центра повернуть заготовку так, чтобы один из профилей зуба шестерни с Z₁ совпал с полюсом П. При этом необходимо следить за тем, чтобы линия зацепления была нормалью к профилю зуба. В этом положении зуб шестерни копируется карандашом на кальку.

19. Центр заготовки колеса совместить с центром О₂, к точке П подвести профиль зуба колеса с Z₂ так, чтобы он вошел в сцепление с зубом шестерни. Зубья колеса с Z₂ также копируются карандашом на кальку.

20. Отметить точки пересечения В₁ и В₂ линии зацепления с окружностями вершин колес. Линия В₁В₂ будет активной линией зацепления длиной q_α. Отметить длину q_f дополюсной части и длины q_a заполюсной части активной линии зацепления.

21. Отметить угол зацепления α_w.

22. Из центров О₁ и О₂ провести дуги радиусами О₁В₁ и О₂В₂, определяющими фактические рабочие профили зубьев mn и ef.

23. Из центров О₁ и О₂ провести начальные окружности (r_w1, r_w2) обоих колес. Отметить h_wa1, h_wf1 – высоту начальной головки и ножки зуба колеса без смещения; h_wa2, h_wf2 – высоту начальной головки и ножки зуба колес с положительным смещением.

24. Отметить радиальный зазор С.

25. Построить дугу зацепления cd: с началом (точка В₁) и концом (точка В₂) зацепления совмещается один из профилей зубьев колеса с положительным смещением и копируется на кальку. Отметить точки пересечения с и d этого профиля с основной окружностью. Дуга cd будет дугой зацепления по основной окружности.

26. Вычислить и занести в отчет и на чертеж зубчатой передачи коэффициент перекрытия:

где В₁В₂ – длина активной линии зацепления ; p_в – шаг зубьев по основной окружности.

1. Все результаты работы занести в отчет лабораторных работ. Вычерченную схему зубчатой передачи и заготовки на чертежной бумаги приложить к отчету.

Контрольные вопросы

- Что называют модулем зацепления?

- Что такое производящий исходный контур?

- Что называют окружностями: делительной, основной, вершин, впадин, начальной?

- Как вычислить диаметр делительной окружности?

- В чем состоит явление подрезания зубъев и каковы критерии подреза?

- В чем состоит явление заострения зубъев и каковы критерии заострения?

- Что называется коэффициентом смещения и смещением исходного производящего контура?

- Что такое коэффициент наименьшего смещения?

- Как вычисляется величина смещения?

- Как вычислить коэффициент смещения?

- Как расположена делительная прямая рейки относительно делительной окружности колеса при различных видах смещения?

- Какое смещение называется нулевым, положительным, отрицательным?

- На какие геометрические параметры збчатого колеса влияют коэффициенты смещения?

- Каким ограничениям должен удовлетворять коэффициент смещения, чтобы получить профиль зуба без подреза и без заострения?

- Что такое модуль m?

- Что называется эвольвентой?

- Назовите свойства эвольвенты.

- Для любой точки эвольвенты показать радиус кривизны и текущий радиус-вектор?

- Для любой точки эвольвенты показать профильный угол и эвольвентный угол.

- Что такое полюс зацепления, линия зацепления, угол зацепления?

- Что такое активная линия зацепления?

- Покажите на рисунке зубчатой передачи радиальный зазор, чему он равен?

- Определите делительное межосевое расстояние зубчатой передачи?

- Какая прямая называется делительной прямой исходного производящего контура (ИПК)?

- Что такое блокирующий контур?

- Какие факторы влияют на выбор коэффициентов смещения зубчатых колес передачи?

- Как вычислить шаг зубчатого колеса по делительной окружности?

- Как изменится делительная толщина зуба и толщина зуба по окружности вершин при увеличении коэффициента смещения?

- Какой должна быть толщина зуба по окружности вершин у зуба без заострения?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Строительная механика

00:00:00