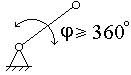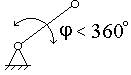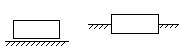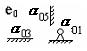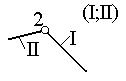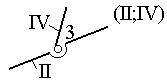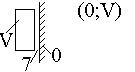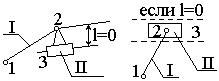Главная

Лабораторная работа №6

Составление кинематической и структурной схемы и структурный анализ механизма

Цель работы.

1.Изучить условные обозначения звеньев и кинематических пар согласно ГОСТ 2.770–68, освоить методику составления кинематической схемы механизма по его макету; научиться определять число и вид звеньев и кинематических пар; освоить методику построения подробной и укрупненной структурных схем механизма, а также конфигурации структуры механизма.

2.Усвоить принцип строения механизмов, сформулированный проф. Ассуром, изучить классификацию групп Ассура и методику структурного анализа. Научиться разделять механизм на статически определимые составные части на основе выделения групп Ассура.

3.Определить число избыточных связей в механизме по структурным формулам А.П. Малышева и О.Г. Озола. Определить число и вид избыточных связей матричным методом. Заменой кинематических пар устранить избыточные связи, чтобы получить рациональный механизм, не имеющий избыточных связей.

Составление кинематической схемы механизма

Механизм – это система тел, предназначенная для преобразования движения одного или нескольких тел в требуемое движение других тел.

Одно или несколько жестко соединенных твердых тел, входящих в состав механизма, называются звеном. Звено, принимаемое за неподвижное, называется стойкой.

Кинематической парой называется соединение двух соприкасающихся звеньев, допускающее их относительное движение.

Совокупность поверхностей, линий, точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется элементом звена (элементом кинематической пары).

Узел сопряжения – это совокупность поверхностей, линий, точек звена, по которым оно в данный момент соприкасается с другим звеном, образуя кинематическую пару. Узел сопряжения это часть элемента звена, которая непосредственно соприкасается с другим звеном.

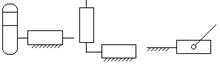
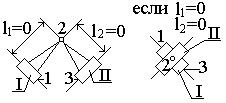
Элементами звеньев четырех подвижной кинематической пары, показанной на рис.1, а, служат наружная цилиндрическая поверхность одного звена и плоскость второго. Узлами являются два отрезка прямых, принадлежащие элементам звеньев и находящиеся в непосредственном контакте. Для кинематической пары, приведенной на рис.1, б, элементы звеньев – это наружная и внутренняя цилиндрические поверхности. Для втулки узел сопряжения и элемент кинематической пары совпадают - это ее внутренняя цилиндрическая поверхность. Для вала узлом служит та часть элемента звена (его внешней цилиндрической поверхности), которая в данный момент непосредственно контактирует с узлом сопряжения втулки.

б) а)

Рис.1. Образованные звеньями кинематические пары, элементы и узлы сопряжения звеньев

Кинематические пары бывают высшие и низшие. Низшие кинематические пары – это пары, звенья которых соприкасаются по поверхности, (узлы сопряжения представляют собой поверхности). Низшие кинематические пары бывают вращательные и поступательные и в плоских механизмах допускают только одну подвижность. Высшие кинематические пары – это такие пары, звенья которых имеют контакт по линии или по точке (узлы сопряжения звеньев - точки или линии).

Совокупность звеньев, соединенных кинематическими парами, представляет собой кинематическую цепь. Кинематические цепи подразделяются на простые и сложные, замкнутые и незамкнутые.

Механизмы, применяющиеся в инженерной практике, образованы замкнутыми кинематические цепями. Поэтому механизмом называется замкнутая кинематическая цепь, в которой при заданном движении одного или нескольких звеньев (ведущих) относительно стойки все остальные звенья (ведомые) совершают однозначно определенные движения.

Для изучения механизма необходимо знать число и виды кинематических пар, число звеньев, их основные размеры и взаимное расположение. Все это изображается на кинематической схеме механизма условными обозначениями пар и звеньев. Условные обозначения установлены ГОСТ 2.770–68. Основные виды звеньев и кинематических пар приведены в таблицах 1и 2.

Таблица 1. Основные виды звеньев, используемых в механизмах

Наименование	Определение	Внешний вид и условное обозначение на кинематической схеме
Стойка	Звено, принимаемое за неподвижное
Кривошип	Вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси.
Коромысло	Вращающееся звено рычажного механизма, которое может совершать только неполный оборот вокруг неподвижной оси.
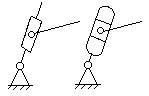
Кулиса	Звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару.
Ползун	Звено рычажного механизма, образующее поступательную пару со стойкой.
Шатун	Звено рычажного механизма, образующее кинематические пары только с подвижными звеньями.
Кулачок	Звено, имеющее элемент высшей пары, выполненный в виде поверхности переменной кривизны.

Таблица 2. Основные виды кинематических пар

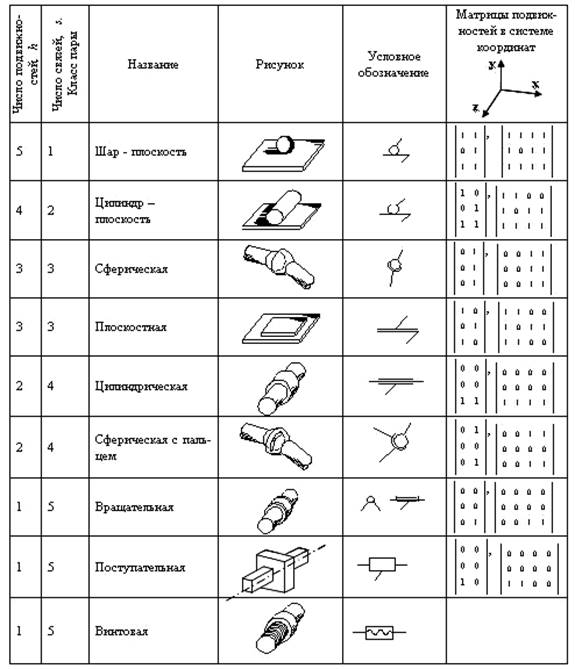
Матрица подвижностей кинематической пары имеет вид:

где – поступательные подвижности вдоль осей X,Y,Z, – вращательные подвижности вокруг осей X,Y,Z. Со знаком “+” и “-” указаны поступательные подвижности в положительном и отрицательном направлениях вдоль осей X,Y,Z и вращательные подвижности, направленные против и по часовой стрелке во круг этих осей.

Кинематическая схема - это модель механизма, отражающая его строение и основные геометрические свойства его звеньев.

Кинематическая схема может отражать строение механизма в масштабе или без соблюдения масштаба. В первом случае кинематическая схема должна показывать все параметры, необходимые для кинематического исследования механизма (длины звеньев, расстояния между центрами шарниров, расстояния до неподвижных направляющих, углы между плечами звеньев и т.д.). Конструктивные особенности механизма на кинематических схемах не показывают, чтобы не усложнять чертеж.

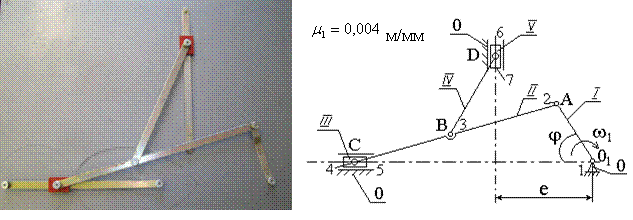
Рис.2. Макет механизма (слева) и его кинематическая схема

Используя размеры звеньев и метод засечек, кинематическую цепь механизма вычерчивают в масштабе на чертеже или с помощью какого-либо графического пакета (КОМПАC, AutoCAD, …). На рис.2 показана кинематическая схема плоского шарнирно-рычажного механизма для преобразования вращательного движения в поступательное, вычерченная в масштабе для заданного положения начального звена I. Масштабный коэффициент длины кинематической схемы механизма м/мм. Масштабный коэффициент длины определяется как отношение реальной длинны звена (в метрах) к длине отрезка ОА (в миллиметрах), изображающего его на кинематической схеме, например,. На примере этого механизма рассмотрим порядок структурного анализа по Ассуру, выявление избыточных связей и их устранение.

Параметры звеньев (размеры даны в метрах) для построения кинематической схемы механизма приведены в таблице 3.

Таблица 3. Параметры звеньев механизма

	е
60	0,16	0,1	0,4	0,2	0,24

Кроме кинематической схемы может быть построена структурная схема механизма. Структурная схема – это модель механизма (изделия), отражающая его строение. Кроме кинематической и структурной схемы для механизмов, как и для других изделий, может быть построена конфигурация структуры. Под конфигурацией изделия понимается представление совокупности его составных частей в виде иерархического дерева.

Определение строения механизма

Для определения строения механизма необходимо установить его состав, т.е. множество входящих в него звеньев и структуру, определяемую совокупностью связей между звеньями, создаваемых кинематическими парами.

Выполняется анализ звеньев и кинематических пар механизма по результатам, которого заполняются таблицы звеньев и кинематических пар.

Виды звеньев и кинематических пар, изучаемого механизма (рис.2), показаны в таблицах 4 и 5.

Структурная схема звена представляет собой граф несвязных вершин, каждая из которых соответствует узлу сопряжения или элементу звена.

Вершины графа соответствующие узлам одного звена, выделяются замкнутой линией, не являющейся элементом графа.

Первая цифра индекса в обозначении узла сопряжения указывает номер звена , которому принадлежит данный узел, второй – номер звена , с узлом сопряжения которого данный узел звена образует кинематическую пару.

Соединение узлов сопряжения, в результате которого звенья образуют кинематическую пару, на её структурной схеме показано ребром, связывающим вершины графа, соответствующие соединяемым узлам (таблица 5).

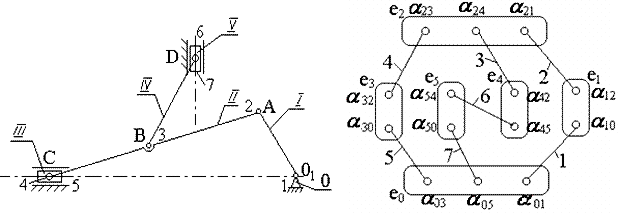
Рис.3. Кинематическая (слева) и структурная схемы механизма

На основе структурных схем звеньев и кинематических пар строится структурная схема механизма, которая вообще не учитывает геометрические свойства его звеньев. Структурная схема механизма показана на рисунке 3.

Таблица 4. Таблица звеньев механизма.

№ звена	Наименование звена	Условное изображение звена на кинематической схеме	Структурная схема звена
O	Стойка
I	Кривошип
II	Шатун
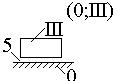
III	Ползун
IV	Шатун
V	Ползун

Таблица 5. Таблица кинематических пар механизма

№ пары	Звенья, образующие кинематическую пару	Структурная схема кинематической пары	Наименование кинемат. пары
1			Вращательная
2			Вращательная
3			Вращательная
4			Вращательная
5			Поступательная
6			Вращательная
7			Поступательная

Структурный анализ механизма по Ассуру

Строение плоского рычажного механизма по Л.В. Ассуру определяет методику его кинематического и силового расчета. Поэтому очень важно уметь проводить структурный анализ механизма. По классификации Ассура каждый плоский рычажный механизм, т.е. механизм с низшими парами, состоит из начального механизма и структурных кинематических групп.

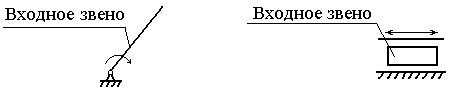
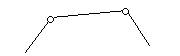
Рис.4. Варианты начальных механизмов

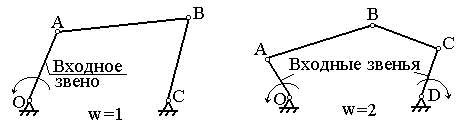
Рис.5. Механизм и их входные звенья

Начальным механизмом называется кинематическая цепь, содержащая стойку и связанные с ней одноподвижными кинематическими парами начальные звенья (рис.4). В качестве начальных звеньев обычно принимаются входные звенья механизма (см. рис.5), т.е. звенья которым сообщается заданное движение. Начальный механизм обладает степенью подвижности w, равной степени подвижности механизма в целом.

Механизмы, образованные присоединением нескольких групп к начальному механизму, обладают степенью подвижности, равной подвижности начального механизма. Присоединенные группы Асура имеют нулевую подвижность и не изменяют подвижность механизма.

Структурной кинематической группой или группой Ассура называется простейшая кинематическая цепь, имеющая нулевую подвижность относительно тех звеньев, к которым она присоединяется, поэтому число кинематических пар группы (р) связано с числом ее звеньев (n) соотношением

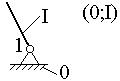
Простейшая группа Ассура состоит из двух звеньев и трех кинематических пар и называется группой 2-го класса. Существует пять видов структурных групп 2-го класса (табл.6).

Таблица 6. Виды структурных групп 1-го класса

Класс группы	Порядок группы	Число звеньев	Число кинем.пар	Вид группы	Кинематическая схема структурной группы 2-го класса 2-го порядка
2	2	2	3	1-й
2	2	2	3	2-й
2	2	2	3	3-й
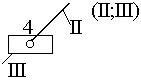
2	2	2	3	4-й
2	2	2	3	5-й

Класс группы равен числу её внутренних кинематических пар, образующих замкнутый контур.

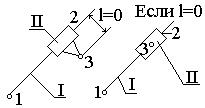
Порядок группы равен числу ее внешних пар, которыми она присоединяется к основному механизму. Структурные группы 2-го класса всегда имеют 2-й порядок, так как присоединение их к основному механизму осуществляется двумя внешними кинематическими парами. На рис.6,а представлена структурная группа 3-го класса 3-го порядка, состоящая из 4-х звеньев и 6-ти кинематических пар. Звено III, входящее в три кинематические пары, называется базисным. На рис.6,б показана структурная группа 4-го класса 2-го порядка, состоящая из 4-х звеньев и 6-ти кинематических пар. Звенья I и IV являются базисными.

Класс механизма определяется наивысшим классом входящей в него структурной группы. Механизм, в состав которого входят группы не выше 2-го класса, называется механизмом 2-го класса. Механизм, в состав которого входят группы не выше 3-го класса, называется механизмом 3-го класса и т.д.

а) б)

Рис.6. Примеры структурных групп Ассура

Методика выделения в механизме групп Ассура

Рассмотрим кинематическую схему механизма (см.рис.7). Степень подвижности механизма определим по формуле Чебышева

где n=5 - число подвижных звеньев; - число низших кинематических пар; - число высших кинематических пар.

Рис.7. Разделение механизма на группы Ассура:

а – разделение кинематической схемы механизма;

б – разделение структурной схемы механизма

При структурном анализе отделяем сначала структурную группу 2-го класса 2-го вида, состоящую из двух звеньев (IV, V) и трех кинематических пар (3, 6, 7). Затем отделяем следующую структурную группу 2-го класса 2-го вида, состоящую из двух звеньев (II, III) и трех кинематических пар (2, 4, 5). Остается начальный механизм, имеющий W=1 и состоящий из ведущего звена I и стойки, связанных кинематической парой 1. На рис.7 разделение механизма на составные части показано на его кинематической и структурной схемах. На рис.8 приведены его составные части.

На рис.8,б показаны структурные схемы кинематических групп, включающие структурные модели соответствующих звеньев и кинематических пар.

Рис.8. Составные части механизма: а – кинематические схемы групп Ассура; б – структурные схемы групп Ассура;

в – составные части (сборочные единицы), выделенные в результате структурного анализа по Ассуру;

г – подробные структурные модели составных частей; д – укрупненные структурные схемы составных частей

Выделение в механизме групп Ассура – это условное разделение его на кинематические цепи, для которых можно проводить силовое и кинематическое исследование, рассматривая их как самостоятельные объекты.

Реально механизм можно разбить на составные части (см. рис.8, в), включающие те же звенья, что входят в соответствующую группу Ассура. В эти составные части входят звенья, а значит образованные ими внутренние кинематические пары групп и узлы сопряжения, которыми составная часть присоединяется к остальной части механизма.

Отличие между составными частями механизма и кинематическими группами Ассура легко увидеть, сравнив их структурные схемы, показанные на рис.8 б и рис.8 г.

На рис.8, д показаны укрупненные структурные схемы составных частей механизма, отражающие только узлы сопряжения, служащие для присоединения составной части к другим компонентам механизма. Они получаются из структурных схем, показанных на рис.8 г, исключением узлов сопряжения, образующих внутренние кинематические пары, и объединением всех звеньев составной части в одно целое.

Таким образом, механизм состоит из начального механизма и двух групп Ассура 2-го класса 2-го вида. Запишем формулу строения механизма в порядке присоединения групп Ассура к начальному механизму:

где в скобках римскими цифрами указаны номера звеньев, составляющих первичный механизм (он отнесен к первому классу) и группы Ассура, а арабскими цифрами – класс групп Ассура. Так как в механизме присутствуют группы не выше 2-го класса, то механизм относится к механизмам 2-го класса. На рис.9 показано строение механизма, представленное его структурной формулой и укрупненной структурной схемой, раскрывающей соединения между составными частями.

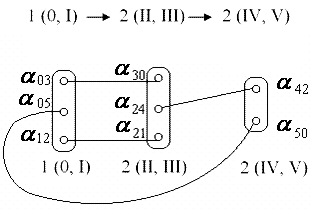
Рис.9. Строение механизма, выявленное в результате

Структурного анализа по Ассуру

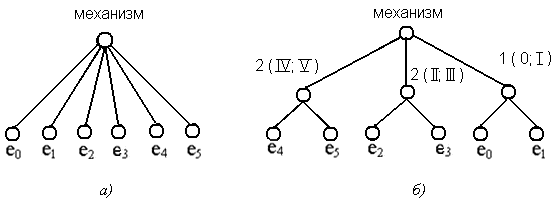
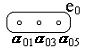
Рис.10. Конфигурация механизма

На рисунке 10 приведены две конфигурации механизма. В первой (рис.10,а) составными частями механизма считаются звенья. Второй вариант конфигурации построен из предположения, что составными частями первого уровня разукрупнения механизма являются сборочные единицы, выделенные в результате структурного анализа по Асуру. На втором уровне разукрупнения располагаются звенья, вошедшие в сборочные единицы. Рис. 10 показывает, что одной и той же структуре механизма (изделия) могут соответствовать разные его конфигурации.

Выявление избыточных связей и их устранение

Для повышения надежности рекомендуется применять механизмы статически определимые, т.е. без избыточных (пассивных) связей. Такие механизмы называют рациональными.

Избыточные (пассивные) связи – это связи, устранение которых не увеличивает подвижности механизма. Они вредны, так как увеличивают требования к точности изготовления звеньев, снижают надежность работы механизма.

Проверить механизм на наличие в нем избыточных связей можно путем подсчета их по структурным формулам, одна из которых предложена А.П. Малышевым:

где q - число избыточных связей; w – степень подвижности механизма; n – число подвижных звеньев; p₅ – число кинематических пар 5-го класса; р₄– число кинематических пар 4-го класса; …..р₁ – число кинематических пар 1–го класса.

Другую формулу предложил О.Г. Озол

Q=w+6к-h,

где к – число независимых контуров в механизме к=p-n; h – суммарное число подвижностей, допускаемых кинематическими парами механизма

При конструировании рационального механизма надо уметь определить в каком замкнутом контуре имеются избыточные связи и какие они. Сделать это можно используя матричный метод определения структурных свойств механизма. Формула Озола и Малышева позволяют установить лишь число избыточных связей в механизме.

Матричное уравнение для определения избыточных связей механизма имеет вид

где

Q – матрица избыточных связей механизма. Отрицательные элементы этой матрицы показывают избыточные связи, положительные – не выявленные подвижности. Н – суммарная матрица подвижностей в кинематических парах. W_O- суммарная матрица общих подвижностей. W_M – суммарная матрица местных подвижностей звеньев; n, p, m – число подвижных звеньев, кинематических пар и начальных звеньев в механизме. Н_i – матрица подвижности i – й кинематической пары. W_Oj - матрица общих подвижностей j–го начального звена (множество ее компонентов, равных единице, является подмножеством равных единице компонентов матрицы подвижностей кинематической пары, связывающей j – е начальное звено и стойку); W_Ml – матрица местных подвижностей l – го звена. F – единичная матрица замыкания контура (матрица подвижностей свободного твердого тела):

Для выявления избыточных связей следует заменить отсутствующие поступательные и вращательные подвижности имеющимися поступательными и вращательными подвижностями вдоль осей не перпендикулярных направлениям отсутствующих подвижностей. Кроме того, отсутствующие поступательные подвижности необходимо заменить имеющимися в наличии вращательными в соответствии с таблицей 7.

Таблица 7. Таблица замены поступательных подвижностей вращательными

	tx	ty	tz
rx		_	_
ry	_		_
rz	_	_	_

Таким образом, в матрице подвижностей отрицательные элементы первого столбца могут быть заменены положительными элементами второго столбца, лежащими в других строках, например:

Одной угловой подвижностью можно заменить только одну отсутствующую поступательную подвижность, отмеченную в матрице отрицательным значением соответствующего элемента. В результате матрица преобразуется к виду:

Рассмотрим пример исследования подвижностей и избыточных связей для механизма, кинематическая схема которого показана на рис.11.

Заданный механизм имеет: n=5 – число подвижных звеньев; – число низших кинематических пар; w=1 степень подвижности.

Для всех звеньев рассматриваемого механизма местные подвижности отсутствуют, и суммарная матрица местных подвижностей имеет вид:

Суммарная матрица общих подвижностей:

Рис.11

Все кинематические пары 5-го класса (классы пар обозначены римскими цифрами и даны в числителе на рис.11).

Определим число избыточных связей по формуле Малышева:

Определим по формуле Озола число избыточных связей.

Здесь

Сумма подвижностей для семи кинематических пар 5-го класса будет равна семи, так как каждая пара имеет по одной подвижности.

Тогда

Мы установили только число избыточных связей в механизме.

Матричный метод позволяет определить какие избыточные связи имеются в механизме. Матрицы подвижностей кинематических пар имеют вид:

Суммарную матрицу подвижностей кинематических пар найдем:

Произведем замену отсутствующих поступательных подвижностей угловыми:

Откуда можно сделать вывод, что две избыточные связи вызваны отсутствием поступательных подвижностей вдоль оси Х, две - отсутствием вращательной подвижности вокруг оси Y и еще две - отсутствием вращательной подвижности вокруг оси Z.

Для устранения избыточных связей выполним замену кинематических пар. Устранение избыточных связей требует уменьшения класса кинематических пар. Для сравнения рассмотрим вариант механизма (см. рис.11), у которого: 1-я кинематическая пара - вращательная 5-го класса; 2-я кинематическая пара – сферическая 3-го класса; 3-я кинематическая пара – вращательная 5-го класса; 4-я кинематическая пара – сферическая 3-го класса; 5-я кинематическая пара - поступательная 5-го класса; 6-я кинематическая пара - сферическая 3-го класса; 7-я кинематическая пара – поступательная 5-го класса. На рис.11 обозначение классов измененных кинематических пар приведено в знаменателе. Матрицы подвижностей сферических кинематических пар имеют вид:

Определим число избыточных связей по формуле Малышева:

Определим число избыточных связей по формуле Озола:

Убедимся, что избыточные связи отсутствуют, используя матричный метод:

Для механизмов, в которых используются только кинематические пары 3, 4 и 5-го класса, можно использовать простое соотношение, облегчающее правильный выбор классов кинематических пар кинематических групп Ассура. Кинематическая группа не вносит избыточных связей при присоединии к механизму, если для нее выполняется соотношение:

где и – число кинематических пар третьего и пятого класса группы Ассура; - число местных подвижностей ее звеньев. При получим:

Данные соотношения будут выполняться и в том случае, когда все кинематические пары четвертого класса, а местные подвижности звеньев отсутствуют. Приведенная зависимость позволяет правильно соориентироваться при выборе классов кинематических пар групп Ассура. Проверку структурных свойств полученного механизма и уточнение классов кинематических пар следует провести используя матричный метод.

Оборудование

Макеты механизмов, масштабная линейка, транспортир, циркуль, карандаши.

Последовательность выполнения работы

1. Ознакомиться с моделью механизма, установить его назначение (например, преобразование вращательного движения в поступательное), определить число звеньев и кинематических пар. Составить кинематическую схему механизма без учета масштаба, обозначив на ней размеры, подлежащие измерению.

2. Измерить расстояние между центрами шарниров, расстояние до неподвижных направляющих, углы между плечами звеньев. Составить таблицу параметров звеньев механизма.

3. Выделить неподвижные элементы кинематических пар, принадлежащие стойке (базовые точки и линии) и нанести их на схему с учетом выбранного масштабного коэффициента длинны , указав расстояния в миллиметрах непосредственно на чертеже. За начало координат базовых точек и линий принять центр вращения кривошипа.

4. Вычертить одно из положений ведущего звена, при котором в механизме нет наложения одного звена на другое. Показать стрелкой направление движения ведущего звена.

5. В выбранном масштабе вычертить кинематическую цепь, образованную остальными звеньями механизма, используя метод планов положений звеньев.

6. Пронумеровать звенья римскими цифрами, а кинематические пары – арабскими цифрами. Кроме того, центры вращательных кинематических пар обозначить прописными буквами латинского алфавита. Указать масштабный коэффициент длинны, использованный при построении кинематической схемы.

7. Составить структурную схему механизма.

8. По структурной формуле Малышева определить степень подвижности механизма.

9. Составить таблицы звеньев и кинематических пар, определив вид пары (вращательная или поступательная), а также указать номера звеньев, образующих эти пары.

10. Провести структурный анализ по Ассуру:

а) разбить механизм на группы Ассура (w=0);

б) каждую группу вычертить в том виде, в каком она изображена на схеме механизма, а также нарисовать структурные схемы (детльную и укрупненную) составных частей механизма, выделенных на основе структурных группы.

в) для каждой группы определить:

- число подвижных звеньев n,

- число низших кинематических пар p_H,

- степень подвижности w,

- класс группы,

- вид (модификацию), если группа 2-го класса.

11. Написать формулу строения механизма.

12. Определить класс и порядок механизма.

13. Нарисовать укрупненную структурную схему механизма.

14. Нарисовать конфигурации механизма: а) считая, что составными частями первого уровня разукрупнения являются его звенья; б) считая, что составными частями первого уровня являются сборочные единицы, выделение в результате структурного анализа по Асуру, а составными частями второго уровня – звенья.

Следующие пункты выполняют студенты, у которых нет домашнего задания по структурному анализу механизма матричным методом.

1. В заданном механизме при известных кинематических парах (все кинематические пары 5-го класса) определить число избыточных связей по формулам Малышева, Озола и матричным методом.

2. Выполнить замену кинематических пар с целью полного устранения избыточных связей (q=0). По формулам Малышева, Озола и матричным методом проверить отсутствие избыточных связей.

Контрольные вопросы

1.Что называется машиной, механизмом?

2.Чем звено может отличаться от детали?

3.Входные и выходные звенья, ведущие и ведомые звенья, начальное звено механизма.

4.Особенности звеньев вида: кривошип, коромысло, кулиса, шатун, ползун.

5.Что называется кинематической парой?

6. Чем определяется класс кинематической пары?

7. Что такое элемент звена (элемент кинематической пары)?

8. Что такое узел сопряжения звена?

9. Чем отличается узел сопряжения от элемента звена?

10. Какие кинематические пары являются высшими, низшими?

11. Приведите примеры пар I ,II, III, IV, V класса.

12. Напишите и объясните структурную формулу Сомова – Малышева.

13. Что такое кинематическая группа Ассура?

14. Как связано число звеньев и число кинематических пар группы Ассура?

15. Чем отличаются группы Ассура от составных частей механизма, соответствующих этим группам?

16. Как определяется класс кинематической группы Ассура?

17. Как определяется порядок групп Ассура?

18. Какая кинематическая цепь является статистически определимой?

19. Что такое избыточные (пассивные) связи?

20. Что такое избыточные групповые подвижности звеньев?

21. Зачем необходимо знать, где и какие возникают лишние связи и избыточные местные подвижности?

22. По какой формуле можно определить число избыточных связей в механизме?

23. Как устранить лишние пассивные связи и избыточные местные подвижности?

24. Как проявляются при сборке избыточные связи?

25. Напишите матрицу подвижностей кинематической пары: вращательной, поступательной, сферической и т.д.?

26. Какие элементы матрицы структурных параметров показывают избыточные связи, а какие избыточные групповые подвижности звеньев?

27. Что такое местные подвижности звеньев?

28. Когда возможна замена отсутствующих поступательных подвижностей вращательными?

29. Что такое кинематическая схема, структурная схема и конфигурация механизма?

30. Как определить число степеней свободы плоского механизма?

31. Как влияют дополнительные связи на подвижность механизма?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Строительная механика

00:00:00