Главная

Лабораторная работа №24

Кинематический анализ зубчатых механизмов

Цель работы: выработка навыков в составлении кинематических схем зубчатых механизмов и определении их передаточных отношений.

1. Определение передаточного отношения аналитическим путем

1.1. 3убчатые механизмы с неподвижными осями

Передаточным отношением называется отношение угловой скорости звена "k" к угловой скорости звена "":

(см. [1, с.365, 402…413]; [2, с.116, 138…166]; [3, с.52…57]).

Для плоского механизма, состоящего из двух зубчатых колес и стойки, имеем:

где n – об/мин, частота вращения;

z – число зубьев;

– радиус начальной окружности.

Условно поставленный знак "минус" показывает, что зацепляющиеся колеса вращаются в разные стороны при внешнем касании (рис.1, а), а знак "плюс" показывает, что колеса вращаются в одном направлении при внутреннем касании (рис.1.1, б).

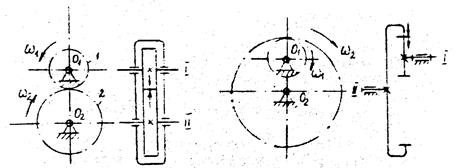
а) б)

Рис.1

Осуществление в одноступенчатых передачах больших передаточных отношений (примерно > 8) становится нецелесообразным, так как диаметр одного из колес получается очень большим. При применяют двухступенчатые зубчатые передачи, при > 40 – трехступенчатые.

Передаточное отношение многоступенчатой передачи равно произведению частных передаточных отношений отдельных ступеней (простых механизмов).

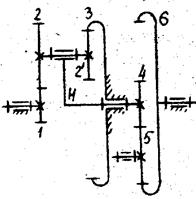
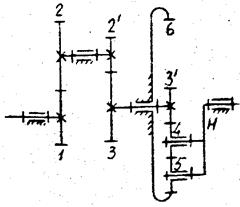
Для ступенчатого механизма, изображенного на рис.2, передаточное отношение определяется по формуле:

Рис.2

Вследствие параллельности валов I и V найденному передаточному отношению, как и в случае одноступенчатой передачи, приписываем знак. Его определяем по правилу стрелок. В нашем случае величине должен быть приписан знак "минус".

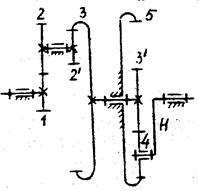
Пример 1. Задана четырехступенчатая передача (рис.3), представляющая привод от электродвигателя к станку. Числа зубьев колес: z₁ = 18, z₂ = 27, z₃ = 12, z₄ = 24, z₅ = 19, z₆ = 57.

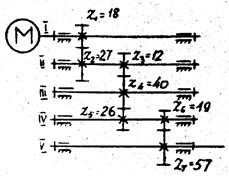
Рис.3

Определить частоту вращения ведомого вела V, если частота вращения вала двигателя = 1440 об/мин.

Передаточное отношение:

(четвертое колесо с числом зубьев z₄ является паразитным и не влияет на величину общего передаточного отношения). Показатель степени при –1 равен числу внешних зацеплений (4).

 об/мин.

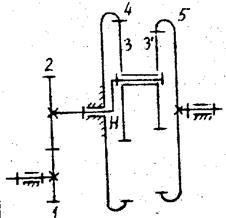
Пример 2.

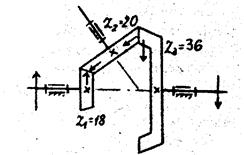
Рис.4

Колеса 1 и 3 вращаются в разные стороны ("правило стрелок").

1.2. Планетарные и дифференциальные зубчатые механизмы

Во всех рассмотренных выше зубчатых механизмах валы зубчатых колес вращались в неподвижных подшипниках, т.е. оси всех колес не меняли своего положения в пространстве. Существуют многоступенчатые зубчатые передачи, оси отдельных колес которых являются подвижными. Такие зубчатые механизмы с одной степенью свободы (W = 1) называется планетарными механизмами, а с числом степеней свободы два и более () – дифференциальными.

Аналитический метод исследования кинематики таких механизмов основывается на способе обращения движения (см. [1, с.406…413]; [2, с.154…166]; [4, с.54…57]). Всем звеньям механизма сообщается дополнительная угловая скорость, которая равна по величине, но противоположна по направлению угловой скорости водила . В результате водило оказывается неподвижным, а дифференциальный (планетарный) механизм превращается в зубчатую передачу с неподвижными осями колес (обращенный механизм).

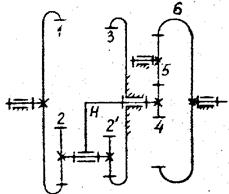
Пример 3. Определить число оборотов водила () и сателлита (), а также направление их вращения, если ведущий вал (колесо 1) вращается с частотой = 60 об/мин. Числа зубьев z₁ = z₃ = 20, z₂ = 40.

Рис.1.5

Модули всех колес одинаковы. Колеса изготовлены без смещения исходного контура. Колесо 4 неподвижно. Колесо 3 обкатывается по колесу 4.

Число степеней подвижности механизма:

где n – число подвижных звеньев;

– число кинематических пар пятого класса,

– число кинематических пар четвертого класса.

Рассматриваемый механизм – планетарный.

Неизвестное число зубьев (z₄) определим из условия соосности:

где – радиусы начальных окружностей, i = 1,…4.

Так как колеса изготовлены без смещения исходного контура, то начальные окружности совпадают с делительными:

Поскольку согласно условию модули всех колес одинаковы, то:

Для определения передаточного отношения применим метод обращения движения. Пусть в рассматриваемом механизме подвижные звенья вращаются с угловыми скоростями . Очевидно, что относительное движение звеньев не изменится, если сообщить всему механизму дополнительное вращение вокруг центральной оси с частотой вращения – n_н (то есть с частотой, равной по величине, но противоположной по направлению вращению водила). Тогда скорости соответственно изменятся и примут значения:

Звено	Фактическая частота вращения	Частота вращения после сообщения механизму дополнительного вращения
Колесо 1	n1
Колесо 4	n4
Водило н	nн

Таким образом, при сообщении всему механизму обращенного движения с частотой – n_н водило будет неподвижным, а планетарный механизм превратится в обыкновенный зубчатый (с неподвижными осями). Передаточное отношение последнего:

или, переходя к угловым скоростям ():

Здесь – фактические угловые скорости, а – угловые скорости в обращенном движении, т.е. угловые скорости обыкновенного зубчатого механизма, полученного из планетарного.

Для обыкновенного зубчатого механизма:

т.к. фактически n₄ = 0.

Знак "плюс" показывает, что входное звено 1 и водило вращаются в одном направлении:

Для определения частоты вращения сателлита:

n₂ = -210 об/мин.

Знак "минус" показывает, что блок сателлитов 2 и 3 и водило вращаются в противоположные стороны.

2. Порядок выполнения работы

В настоящей работе необходимо выполнить кинематический анализ трех зубчатых механизмов, в том числе одного планетарного или дифференциального. Для каждого зубчатого механизма составляется кинематическая схема и определяется передаточное отношение сначала в общем виде, а затем подсчитывается его значение.

Кинематическая схема должна быть составлена грамотно с соблюдением условностей, принятых при составлении кинематических схем (ГОСТ 2.703-74, ГОСТ 2.770-68).

После представления отчета о работе каждый студент должен решить контрольную задачу.

Форма протокола

"КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗУБЧАТЫХ МЕХАНИЗМОВ"

Студент Группа Руководитель

1. Номер механизма _____

Кинематическая схема

Общее передаточное отношение механизма:

а) расчетное значение;

б) полученное экспериментально.

2. Номер механизма _____

Кинематическая схема и т.д.

Работу выполнил Работу принял

Контрольные задачи

Вариант задачи назначается преподавателем.

Недостающие числа зубьев колес определить из условия соосности, считая, что все зубчатые колеса механизма имеют один и тот же модуль и угол зацепления.

Задача № 1 Определить n6	№ вар.	z1	z2	z3	z4	z5	n1
	1 2 3 4 5 6 7 8 9 10	11 14 17 17 13 17 14 17 19 18	19 18 23 29 15 20 28 17 21 22	40 45 51 60 39 58 55 51 54 52	29 12 14 19 15 13 16 14 17 19	24 22 25 33 12 19 16 21 22 15	210 512 128 989 910 309 246 160 610 490

Задача № 2 Определить n5	№ вар.	z1	z2	z3	z4	z5	n1
	1 2 3 4 5 6 7 8 9 10	11 18 24 12 13 16 11 17 17 19	18 32 25 16 17 18 16 30 27 31	40 42 48 36 46 48 38 51 45 57	60 63 63 54 56 78 57 68 80 96	45 79 78 72 68 66 68 88 65 72	540 158 832 320 680 297 288 198 1053 930

Задача № 3 Определить nн	№ вар.	z1	z2	z2'	z3	z3'	z4	n1
	1 2 3 4 5 6 7 8 9 10	11 17 11 16 22 17 21 17 19 23	22 31 18 20 24 21 25 32 30 24	17 16 20 14 18 20 20 16 15 20	51 51 75 70 66 68 63 68 46 50	12 21 18 16 17 15 20 20 23 19	32 28 26 24 34 25 30 25 30 19	550 434 450 300 600 280 450 360 530 480

Задача № 4 Определить nн	№ вар.	z1	z2	z2'	z3	z4'	z5	n1= n5
	1 2 3 4 5 6 7 8 9 10	11 15 19 26 16 14 18 12 13 20	15 25 31 15 30 28 24 24 25 24	18 20 24 19 22 40 14 17 21 26	11 15 14 13 12 15 11 16 17 18	56 63 62 52 55 84 42 64 65 75	14 18 20 13 11 12 14 16 26 15	320 245 589 960 170 110 200 264 380 132

Задача № 5 Определить n6	№ вар.	z1	z2	z2'	z3'	z4	z5	n1
	1 2 3 4 5 6 7 8 9 10	75 72 56 85 70 65 64 84 80 60	35 18 21 30 30 35 16 21 40 30	20 12 14 25 25 15 12 14 30 20	11 15 13 16 19 17 13 18 20 16	13 15 16 19 30 19 13 26 22 16	50 88 59 98 57 85 52 90 86 64	220 100 200 490 780 200 260 150 430 320

Задача № 6 Определить nн	№ вар.	z1	z2	z2'	z3	z3'	z4	z5	n1
	1 2 3 4 5 6 7 8 9 10	36 21 27 24 32 24 29 23 28 22	40 35 38 38 40 32 44 42 42 40	21 18 19 17 19 18 20 15 14 13	30 25 42 30 36 27 40 25 21 26	24 23 21 19 18 20 22 17 16 15	18 17 15 13 23 17 17 12 21 22	14 27 12 23 15 18 12 18 14 11	320 440 320 360 320 420 400 420 630 480

Контрольные вопросы

- Укажите типы плоских и пространственных зубчатых передач в зависимости от расположения осей вращения колес?

- Что такое передаточное отношение, как оно определяется для оноступенчатых передач по величине и знаку?

- Что представляет собой червячная передача? Как определяется число заходов червяка?

- В чем заключается кинематический анализ зубчатого механизма?

- Как аналитически определить передаточное отношение зубчатого механизма?

- Как на опыте определить передаточное отношение зубчатого механизма?

- Какое влияние на передаточное отношение оказывают ряды зубчатых механизмов при различных соединениях звеньев?

- Как влияет на передаточное отношение наличие подвижной оси в зубчатом механизме?

- Ка изменится передаточное число планетарного механизма с ведущим водилом и остановленным опорным колесом, если ведущим звеном будет солнечная шестерня?

- Почему существуют ограничения на величину передаточного отношения для элементарного зубчатого механизма?

- В чем заключается сущность метода обращенного движения?

- Как определяется передаточное отношение ступенчатой зубчатой передачи?

- Как определяется передаточное отношение сложного зубчатого механизма?

- Чему равно число степеней свободы рядового зубчатого механизма, дифференциала?

- В чем состоит особенность ступенчатых передач с промежуточными (паразитными) колесами?

Библиографический список

1. Теория механизмов и машин: Учеб. для втузов / Под ред. К.В.Фролова. М., 1987.

2. Артоболевский И.И. Теория механизмов и машин. М., 1988.

3. Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин. М., 1985.

4. Соколовский В.И. Кинематический анализ и синтез механизмов. Свердловск, 1979.

5. Теория механизмов и машин: Сб. контрольных работ и курсовых проектов / Под ред. Н.В.Алехновича. Минск, 1970.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Строительная механика

00:00:00