Главная

Лабораторная работа №4

Cтруктурный анализ плоских механизмов

Цель работы: изучение принципов структурного построения и анализа механизмов.

1. Теоретическое обоснование

Приступая к анализу существующего или синтезу нового механизма, необходимо прежде всего определиться с его структурой, то есть составить кинематическую схему, подсчитать количество подвижных звеньев определить характер их соединения друг с другой, уяснить метод образования механизма и чётко представить себе схему передачи движения от ведущих звеньев к ведомым.

1.1. Механизмом называется искусственно созданная система, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел (звеньев). Определенность движения звеньев в механизме обеспечивается тем, что они, соединяясь между собой кинематическими парами, образуют кинематические цепи.

1.2. Звеном называется деталь или несколько неподвижно соединенных друг с другом деталей, которые движутся как одно целое. В Приложении 1 показаны условные изображения различных звеньев механизма и их названия.

1.3. Кинематической парой называют соединение двух соприкасающихся звеньев, допускающее их относительное движение. При этом число возможных независимых движений H одного звена относительно другого называют числом подвижностей кинематической пары, а ограничения, наложенные на относительное движение звеньев в кинематической паре – условиями связи. Условные изображения наиболее распространенных кинематических пар даны в Табл.1.

1.4. Кинематические пары классифицируются по следующим признакам:

а) по числу степеней свободы H звена кинематической пары в относительном движении выделяют одноподвижные, двухподвижные, трехподвижные, четырехподвижные и пятиподвижиые. Подвижность кинематической пары определяется зависимостью H=6-S, где 6 – максимальное число возможных движений твердого тела в пространстве: трех поступательных по осям и трех вращательных вокруг осей координат XYZ; S – число условий связи, наложенных кинематической парой на относительное движение каждого звена.

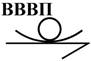
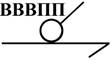
б) по характеру соприкосновения звеньев кинематические пары различаются на низшие и высшие.

Таблица 1

№ п/п	Условное изображение кинематических пар	Возможные виды относительного движения	Название кинематической пары
1		В	Вращательная пара с одним неподвижным звеном
2		В	Вращательная пара с двумя подвижными звеньями
3		П	Поступательная пара с одним неподвижным звеном
4		П	Поступательная пара с двумя подвижными звеньями
5		В	Звено в различных вариантах, входящее одновременно в состав двух или трех одноподвижных вращательных пар
6		ВВВ	Трехподвижная пара – сферический шарнир
7		ВВ	Двухподвижная пара – сферический шарнир с пальцем

Пояснения: В – вращательное относительное движение; П – поступательное относительное движение.

в) по характеру относительного движения звеньев одноподвижные кинематические пары подразделяются на вращательные – В, поступательные – П и винтовые.

Низшими парами называются такие пары, в которых соприкосновение элементов происходит по поверхности. Например, одноподвижные поступательная и вращательная пары, а также двухподвижная цилиндрическая и трехподвижная сферическая.

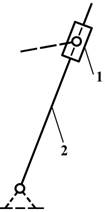
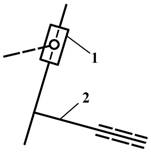
Высшими называются такие кинематические пары, у которых соприкосновение элементов пары происходит по линии или в точке. Например, кулачок и ролик толкателя кулачкового механизма (рис.1,а) и зубья зубчатых колес (рис.1, б).

В Приложении 2 представлены примеры различных кинематических пар. Возможные независимые движения показаны стрелками и буквенными сочетаниями.

а) б)

Рис.1. Высшие плоские двухподвижные кинематические пары.

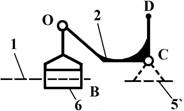
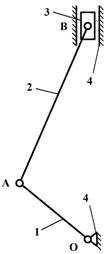
1.5. Кинематической цепью называют систему звеньев, соединенных между собой кинематическими парами. Кинематические цепи бывают замкнутыми (рис.2) и открытыми (рис.3), простыми и сложными, а по виду траекторий движения точек звеньев разделяются на плоские и пространственные. Наибольшее распространение на практике имеют плоские кинематические цепи.

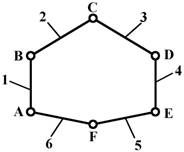
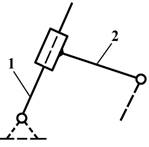
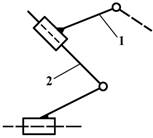
Рис.2. Простая плоская кинематическая цепь

Рис.3. Простая пространственная кинематическая цепь манипулятора

Плоской называется кинематическая цепь, если точки ее звеньев описывают траектории, лежащие в параллельных плоскостях, то есть их траекториями являются плоские кривые. Естественно если точки звеньев описывают пространственные кривые, то такие кинематические цепи (как и кинематические пары) называются пространственными.

Сложной называется кинематическая цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары. Пример такой цепи дан на рис.4, д и рис.9.

1.6. Степенью подвижности кинематической цепи W называют число степеней свободы кинематической цепи относительно стойки – звена, принятого за неподвижное. Для плоских механизмов применяется формула Чебышева

где n - число подвижных звеньев кинематической цепи; p₁ – число одноподвижных кинематических пар; р₂ – число двухподвижных кинематических пар.

В пространственных кинематических цепях степень подвижности определяется по формуле Малышева

Здесь р₃ – число трехподвижных кинематических пар; р₄ – число четырехподвижных кинематических пар; р₅ – число пятиподвижных кинематических пар.

Плоские кинематические цепи с нулевой степенью подвижности называются группами Ассура. Это такие группы звеньев, которые при соединении свободными кинематическими парами со стойкой превращаются в ферму. Группы Ассура имеют только одноподвижные кинематические пары, р₂=0. Тогда степень подвижности выразится

откуда р₁ = 3/2 n.

Возможное число звеньев и кинематических пар в группах Ассура приведено в Табл.2.

Таблица 2

Число звеньев n	2	4	6	8	и т.д.
Число кинематических пар	3	6	9	12	и т.д.
Класс старшего контура	II	III, IV	IV, V	V, VI	и т.д.

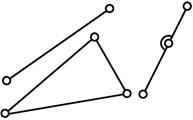
1.7. Группы Ассура делятся по классификации И.И. Артоболевского на классы, порядки и виды. Класс группы задается наивысшим замкнутым контуром, входящим в ее состав. Класс же контура определяется числом внутренних кинематических пар, образующих этот замкнутый контур. Можно сказать, что:

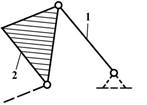
а) в группу Ассура II-го класса входит прямолинейный контур (табл.3);

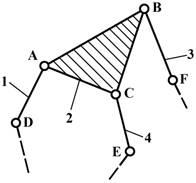
б) в группу Ассура III-го класса – трехсторонний контур ABC (рис.4,б);

в) в группу Ассура IV-го класса – четырехсторонний подвижный контур BCDE.

Таблица 3

Классы контуров
II	III	III	IV	V

Модификации групп Ассура II, III, IV классов представлены на рис.4.

а)	б)		в)
г)		д)

Рис.4. Группы Ассура: а) II-го класса; б) в) г)III-го класса; д) IV-го класса

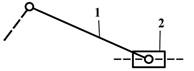
Группы Ассура II класса содержат два звена и три кинематических пары. Разновидности групп Ассура II класса изображены на рис.5:

вид 1 – все кинематические пары вращательные;

вид 2 – одна крайняя кинематическая пара – поступательная, а все остальные – вращательные;

вид 3 – звенья соединены между собой поступательной кинематической парой, а крайние пары являются вращательными;

вид 4 – звенья соединены вращательной парой, а обе крайние кинематические пары – поступательные;

вид 5 – одна крайняя кинематическая пара – вращательная; все остальные – поступательные.

Вид 1	Вид 2	Вид3
	Вид 5
Вид 4

Рис. 5. Группы Ассура II -го класса различных видов.

Порядок группы Ассура определяется количеством кинематических пар, которыми она присоединяется к другим звеньям, т.е. числом ее внешних (свободных) пар.

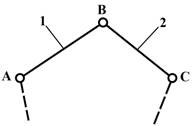
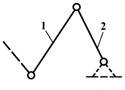
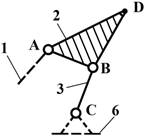
В группе Ассура на Рис.4-б звено 2, называемое базисным, входит в три внутренние кинематические пары со звеньями 1,3 и 4. Звенья 1,3,4 называются поводками и своими внешними кинематическими парами присоединяются к другим звеньям механизма. Эта группа называется трехповодковой, или группой Ассура III класса III порядка.

Лишние степени свободы и пассивные связи

При определении степени подвижности механизма необходимо учитывать наличие лишних степеней свободы и пассивных связей, которые не влияют на характер движения механизма в целом.

Звенья, вносящие пассивные связи, уменьшают степень подвижности механизма, поэтому при определении степени подвижности эти звенья не учитываются.

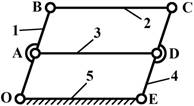
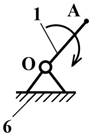
Рис. 6

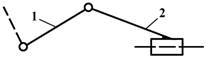
На рис.6 изображен четырехзвенный механизм, у которого звено 3 вносит пассивные связи. Степень подвижности механизма с учетом пассивных связей составляет

Очевидно, что звено 3 введено конструктивно для увеличения жесткости звеньев 1 и 4. Поэтому без учета пассивной связи имеем:

Следовательно, данный механизм имеет степень подвижности W=1. В кулачковом механизме с роликовым толкателем (рис. 1,а) степень подвижности получается

Здесь наблюдается лишняя степень свободы, представляющая собой дополнительную подвижность ролика относительно толкателя. Она не сказывается на степени подвижности кулачкового механизма и W=l.

Принцип образования механизмов

При изучении механизмов их представляют на чертеже в виде структурной или кинематической схем.

Структурной схемой механизма называется графическое изображение механизма с применением условных обозначений звеньев и кинематических пар. Кинематическая схема изображается в масштабе с указанием размеров, необходимых для кинематического расчета механизма. Звенья нумеруются арабскими цифрами в порядке их присоединения к входному звену. Кинематические пары обозначаются заглавными латинскими буквами в последовательности присоединения звеньев.

Входным звеном механизма называется такое звено, закон движения которого задан. Во всяком плоском механизме имеется одно или несколько входных звеньев в виде кривошипа или ползуна (рис.7,а, б). Количество входных звеньев определяется степенью подвижности механизма.

а)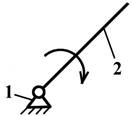 б)

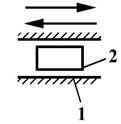
Рис.7

Группа звеньев, состоящая из входного звена и стойки, называется начальным механизмом или механизмом I-го класса. Начальный механизм обладает одной степенью подвижности и дальнейшее наслоение кинематических цепей не должно изменять степени подвижности всего механизма.

Основной принцип образования механизмов, предложенный Л.В. Ассуром, заключается в следующем: любой механизм может быть образован путем последовательного присоединения кинематических цепей с нулевой степенью подвижности сначала к входному звену и к стойке, а затем и к любым другим звеньям. И, наоборот, плоский механизм всегда можно разделить на механизм I-го класса и группы Ассура.

Рассмотреть строение механизма – это значит установить, из каких структурных групп состоит данный механизм, и в какой последовательности они присоединены друг к другу. Для выявления класса механизма необходимо расчленить его на группы Ассура, начиная отсоединение с наиболее удаленных от входного звена. При этом степень подвижности оставшейся части механизма не должна изменяться. Класс всего механизма определяется по наивысшему классу группы Ассура, входящей в механизм.

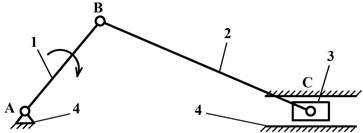
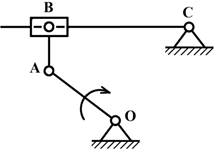
Рис. 8

Строение механизма можно записать в виде структурной формулы, которая указывает состав и последовательность присоединения групп Ассура. Например, для механизма на рис.8, образованного путем присоединения к начальному механизму I-го класса группы Ассура II-го класса, II-го порядка, 2-го вида, структурная формула имеет вид:

где в числителе перечислены звенья, а в знаменателе указаны кинематические пары, входящие в группы звеньев:

I – начальный механизм первого класса;

II – группа Ассура второго класса.

Здесь В_А(1,4), В_В(2,1), В_С(3,2) – индекс вращательных кинематических пар в точках, обозначенных на схеме, с указанием соединяемых звеньев;

П_С(3,4) – индекс поступательной кинематической пары, позволяющей поступательное относительное движение звеньев.

Данный механизм II класса, так как самый высокий класс группы Ассура – второй.

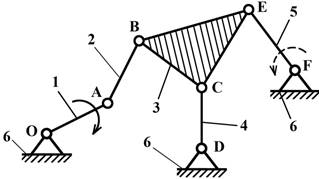
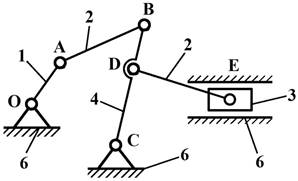
Рис.9

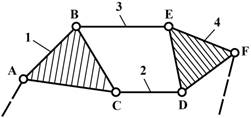
Класс и порядок механизма в некоторых случаях может меняться в зависимости от того, какое звено принято в качестве входного. Если для шестизвенного механизма (рис.9) принять за входное звено 5 (возможно и 4), то весь механизм будет II класса, так как структурная формула имеет вид

а если принять за входное звено I, то невозможно выделить группу звеньев II класса и механизм разбивается на начальный механизм I класса и группу Ассура III класса. Структурная формула выглядит так

Рассмотренное строение плоских механизмов может быть распространено на механизмы, в составе которых имеются и высшие кинематические пары. Для этого каждая пара заменяется кинематической цепью, в состав которой входят только одноподвижные кинематические пары (шарниры и ползуны).

Целью структурного анализа механизмов является определение степени подвижности и его расчленение на группы Ассура.

Замена высших кинематических пар

В тех случаях, когда в механизм входят как высшие, так и низшие кинематические пары, для структурного анализа выполняют замену высших пар кинематической цепью, состоящей из звеньев, входящих только в пары 5-го класса. Одну высшую пару в простейшем случае можно заменить одним звеном, входящим в две низшие пары, расположенные в центрах кривизны профилей, образующих высшую пару. В результате такой замены будут выполнены следующие условия:

во-первых, сохранится прежняя степень подвижности механизма, в котором произведена замена;

во-вторых, характер относительного мгновенного движения звеньев не изменится.

Чтобы заменяющий механизм был кинематически эквивалентным заменяемому, необходимо при замене придерживаться определенных правил, которые заключаются в следующем: если высшая пара представляет касание профилей 1 и 2 (рис.10), то в точке контакта В надо провести нормаль n-n к профилям. На этой линии найти центры кривизны профилей и установить в них шарниры D и Е, соединив их жестким фиктивным звеном 3. Соединяя шарниры D и Е с центрами А и С получим заменяющий механизм – шарнирный четырехзвенник ADEC.

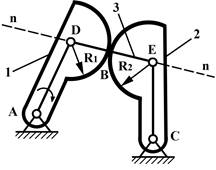
Рис.10

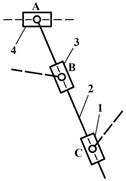
В случае, если один из профилей высшей пары будет прямой линией, центр кривизны его будет удален в бесконечность и фиктивное звено будет входить в одну вращательную и одну поступательную пару. Такая замена показана на рис.11.

а) заменяемый механизм	б) заменяющий механизм
Рис.11

Заменяющие механизмы строятся для структурного и кинематического исследования.

Рассмотрим несколько примеров замены высших пар.

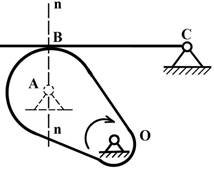
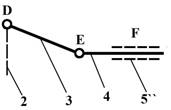
Пример 1. На рис.12, а показан механизм, в котором звенья 1 и 2 образуют высшую пару. Для замены этой кинематической пары проводим общую нормаль в точке касания звеньев и находим центры кривизны, помещаем в них вращательные пары А и В 5-го класса и соединяем их прямой АВ ( и – радиусы кривизны профилей). Заменяющий механизм представлен на рис.12, б.

Для основного механизма (рис.12, а) степень подвижности определяется по формуле Чебышева:

Для заменяющего механизма (рис.1.7, б) степень подвижности равна:

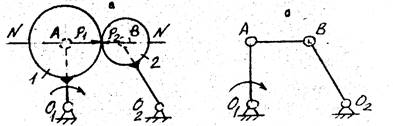
Рис. 12

Пример 2. Рассмотрим механизм, изображенный на рис.13, а. Здесь

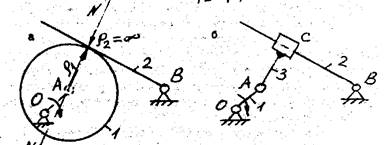
Рис. 13. а) основной механизм; б) заменяющий механизм

Этот механизм можно заменить другим рис.13, б, включающим только низшие кинематические пары. Степень подвижности заменяющего механизма . Заменяющий механизм, обладая той же степенью подвижности, что и основной, не изменяет характера мгновенного относительного движения звеньев.

2. Последовательность выполнения работы

Содержание работы. Студент должен рассмотреть два механизма, при этом следует определить число звеньев и кинематических пар, изобразить структурную схему механизма и составить структурную формулу.

Оборудование: для студентов всех специальностей механизм с низшими кинематическими парами, а для механиков, дополнительно, механизм с высшей кинематической парой.

Инструменты: линейка, треугольник, циркуль и транспортир.

Порядок структурного анализа механизмов

1. Ознакомиться с принципом действия механизма и установить его назначение (Например: преобразовать вращательное движение в поступательное).

2. Определить: какие из звеньев являются кривошипом, шатуном, ползуном, кулисой, коромыслом. Наименование звеньев записать в таблицу основных результатов.

3. Вычертить одно из положений механизма в виде структурной схемы, при котором достаточно наглядно видны все звенья (не будет наложения одного звена на другое). Указать стрелкой направление вращения входного звена – кривошипа.

4. Пронумеровать звенья арабскими цифрами в порядке их присоединения к кривошипу (1,2,3 и т.д.).

5. Обозначить кинематические пары заглавными латинскими буквами в последовательности присоединения звеньев.

6. Определить:

а) число подвижных звеньев (n);

б) тип кинематических пар (В - вращательная, П- поступательная);

в) количество одноподвижных (р₁) и двухподвижных (р₂) кинематических пар;

г) степень подвижности W механизма;

д) наличие пассивных связей и лишних степеней свободы; результаты занести в таблицу.

7. Расчленить механизм на структурные группы Ассура и начальный механизм.

8. Вычертить структурные группы Ассура и начальный механизм с правильным обозначением кинематических пар и звеньев механизма, начиная с наиболее удаленной группы.

9. Определить для каждой группы Ассура: класс, вид, степень подвижности и составить структурную формулу механизма.

10. Определить степень подвижности начального механизма и составить структурную формулу.

11. Составить структурную формулу для механизма в целом.

12. Определить класс всего механизма.

13. Показать на схеме расстояния в мм между неподвижными элементами кинематических пар (базовыми точками на стойке), приняв за начало системы координат центр вращения кривошипа. Определить все размеры между центрами шарниров и результаты записать в таблицу.

14. Подписать и защитить отчет по лабораторной работе.

Форма отчета

"структурный анализ и классификация плоских механизмов"

Студент Группа Руководитель

Цель: Изучение принципов строения и структурного анализа механизмов.

Оборудование: I. Модель механизма с низшими кинематическими парами.

II. Модель механизма с высшей кинематической парой.

Инструменты: Линейка, треугольник, циркуль, транспортир.

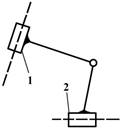
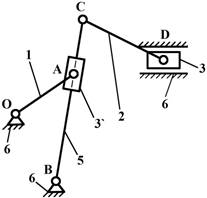
I. АНАЛИЗ РЫЧАЖНОГО ШЕСТИЗВЕННИКА

1) Структурная схема.

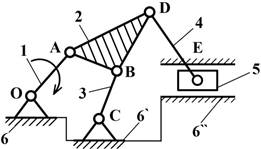
Назначение механизма: преобразовать вращательное движение кривошипа в поступательное движение ползуна с усложненным законом движения.

2) Звенья механизма.

Номер звена	Наименование	Подвижность звеньев	Число подвижных звеньев
1	Кривошип	подвижное	n=5
2	Шатун	– « » –
3	Коромысло	– « » –
4	Шатун	– « » –
5	Ползун	подвижное
6	Стойка	неподвижное

3) Кинематические пары

Обоз- наче- ние	Соеди- няемые элементы	Тип пары			Индекс пары	Число пар
		Вид движения	Характер соединения	Подвижность		одноподвижных	двухподвижных
O A B C D E E	1,6 2,1 3,2 3,6 4,2 5,4 5,6	вращат. – « » – – « » – – « » – – « » – вращат. поступ.	Низшая – « » – – « » – – « » – – « » – – « » – Низшая	Одноподвижн – « » – – « » – – « » – – « » – – « » – Одноподвижн	В(1,6) В(2,1) В(3,2) В(3,6) В(4,2) В(5,4) П(5,6)	p1=7	p2=0

4) Определение степени подвижности механизма

Лишних степеней свободы и пассивных связей нет.

5) Строение групп Ассура.

а)	Последняя группа Ассура II класса, II порядка, 2-го вида Структурная формула:
б)	Предпоследняя группа Ассура II класса, II порядка, 1-го вида Структурная формула:
в)	Начальный механизм I класса Структурная формула:

6) Структурная формула всего механизма:

Данный механизм II класса, так как самый высокий класс группы Ассура – второй.

Работу выполнил________________

Отчет принял__________________

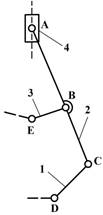
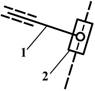
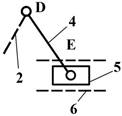
II. МЕХАНИЗМ С ВЫСШЕЙ КИНЕМАТИЧЕСКОЙ ПАРОЙ.

1) На схеме приведен механизм приемника давления электрического дистанционного манометра.

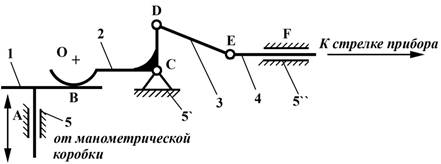
2) Звенья механизма.

Номер звена	Наименование	Подвижность звеньев	Число подвижных звеньев
1	Ползун	подвижное	n=4
2	Коромысло	– « » –
3	Шатун	– « » –
4	Шток	подвижное
5	Стойка	неподвижное

3) Кинематические пары

Обозначение	Соединяемые элементы	Тип пары			Индекс пары	Число пар
		Вид движения	Характер соединения	Подвижность		одноподвижных	двухподвижных
A B C D E F	1,5 1,2 5,2 2,3 3,4 4,5	поступ. вращат. вращат. вращат. вращат. поступ.	Низшая Высшая Низшая Низшая Низшая Низшая	Одноподвижн Двухподвижн Одноподвижн Одноподвижн Одноподвижн Одноподвижн	П(1,5) В(1,2) В(5,2) В(2,3) В(3,4) П(4,5)	p1=5	p2=1

4) Степень подвижности механизма.

5) Строим заменяющий механизм.

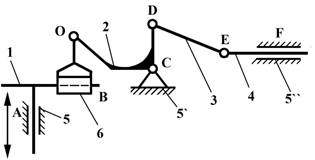
Здесь двухподвижная кинематическая пара в точке В заменена двумя одноподвижными в точках В и О путем введения жесткого фиктивного звена 6. Для заменяющего механизма имеем n =5, p₁ =7, р₂=0 и получаем:

6) Группы Ассура.

а)	Последняя группа Ассура II класса, II порядка, 2 вида n=2, p1=3 и . Структурная формула:
б)	Предпоследняя группа Ассура II класса, II порядка, 2 вида n=2, p1=3 и . Структурная формула:
в)	Начальный механизм I-го класса Структурная формула:

7) Структурная формула всего механизма:

Данный механизм II-го класса, т.к. наивысший класс групп Ассура, входящих в состав механизма – второй.

Контрольные вопросы

- Что такое механизм, звено, кинематическая пара, кинематическая цепь, кинематическая схема, структурная схема?

- Последовательность структурного анализа механизма.

- Формула строения механизма.

- Основной принцип образования механимза.

- По каким признакам делятся кинематические пары на классы и на виды: низшие, высшие?

- Дайте определение механизму, кинематической цепи.

- Чем отличаются плоские механизмы от пространственных?

- Как влияют пассивные связи на степень подвижности механизма?

- Какие звенья образуют механизм I-го класса?

- Как может быть образован механизм?

- Какие кинематические схемы называются группами Ассура (структурными группами)?

- Что характеризует число "степень подвижности механизма"?

- Каков принцип построения новых механизмов?

- По каким признакам классифицируются механизмы?

- По каким признакам классифицируются группы Accypa?

- Как определить класс группы Ассура, ее порядок и вид?

- Какие группы Ассура находят наибольшее распространение?

- Как определить класс всего механизма?

- В какой последовательности механизм разбивается на группы Ассура?

- Чему равна степень подвижности групп Ассура?

- Чему равна степень подвижности механизма I класса (ведущего звена со стойкой)?

- Какие группы являются группами второго, третьего, четвертого класса?

- Какие и сколько видов имеет группа Ассура второго класса?

- Как составляется структурная формула механизма?

- Приведите пример механизма с лишней степенью свободы.

- Укатите возможные причины появления избыточных связей.

- С какой целью производится замена высших пар кинематическими цепями с низшими. парами?

- Укажите условия замены высших пар.

- Приведите пример замены высшей пары.

Библиографический список

1. Фролов К.В., Попов С.А. и др. Теория механизмов и механика машин – учебник для ВТУЗов. М., Высшая школа, 2003.

2. Марченко С.И., Марченко Е.П., Логинова Н.В. Теория механизмов и машин. Ростов н/Д, Феникс, 2003.

3. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин. М., Высшая школа, 2001.

4. Артоболевский И.И. Теория механизмов и машин. М., Наука, 1988.

5. Кореняко А.С. Курсовое проектирование по теории механизмов и машин. Киев, «ВИЩА школа», 1976.

6. Левицкая О.М., Левицкий М.И. Курс теории механизмов и машин. М, Высшая школа, 1978.

7. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. М, Наука, 1975.

8. Иосилевич Г.Б. и др. Прикладная механика – учебник для ВУЗов. М., Высшая школа, 1989.

Приложение 1. Условные изображения и название звеньев механизма

Стойка – это неподвижное звено. В зависимости от характера движения относительно стойки звенья называют:

- кривошипом (АО) – звено 1, которое образует вращательную пару со стойкой и совершает полный оборот вокруг неподвижной оси.

- шатуном (AB,CD) – звено 2 соединенное вращательными парами с подвижными звеньями, но не связанное со стойкой 6;

- ползуном (B, D, E) – звено 3 шарнирно соединенное со звеном 2 и поступательно перемещающееся по неподвижным направляющим;

- коромыслом (ВС) – звено 4, которое совершает неполный оборот вокруг оси, связанной со стойкой;

- кулисой (ВС) – звено 5 вращающееся вокруг стойки 6, которое является направляющей для кулисного камня;

- кулисным камнем (A) – звено 3`, образующее поступательную пару с кулисой.

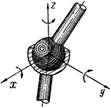
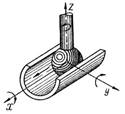
Приложение 2. Примеры кинематических пар и комбинации независимых движений

Тип пар	Название	Возможные движения и условные обозначения	Примеры кинематических пар
Плоские	Одноподвижная, низшая
	Двухподвижная высшая	ВП
Пространственные	Винтовая – одноподвижная, низшая
	Двухподвижная, низшая – цилиндрическая
	Трехподвижная, низшая – сферическая
	Четырехподвижная, высшая – шар-цилиндр
	Пятиподвижная, высшая – шар-плоскость

Приложение 3. Основные понятия, определения и термины

МЕХАНИЗМ – система тел, созданная для преобразования движения одного или нескольких твердых тел в требуемые движения других тел.

МАШИНА – устройство, выполняющее механические движения для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда.

ЗВЕНО – одна или несколько неподвижно соединенных друг с другом деталей, входящих в механизм и движущихся, как одно целое.

КИНЕМАТИЧЕСКАЯ ПАРА – соединение двух звеньев, допускающее их относительное движение. В плоских механизмах встречаются одноподвижные кинематические пары с касанием звеньев по поверхности (низшие – вращательные и поступательные), а также двухподвижные с касанием звеньев в точке (высшие – в зубчатых зацеплениях и кулачковых механизмах).

ЭЛЕМЕНТ КИНЕМАТИЧЕСКОЙ ПАРЫ –совокупность поверхностей, линий и точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару.

СТЕПЕНЬ ПОДВИЖНОСТИ КИНЕМАТИЧЕСКОЙ ПАРЫ – целое число, показывающее сколько независимых движений позволяет делать данная пара одному звену относительно другого. По степени подвижности пары делят на: одноподвижные, двухподвижные, трехподвижные, четырехподвижные и пятиподвижные.

ОДНОПОДВИЖНАЯ ПАРА – кинематическая пара с одной степенью свободы в относительном движении ее звеньев. Одноподвижными являются поступательная, вращательная и винтовая пары.

ДВУХПОДВИЖНАЯ ПАРА – кинематическая пара с двумя степенями свободы в относительном движении ее звеньев. Двухподвижными парами в плоских механизмах считают все высшие пары (зуб+зуб и кулачек+толкатель)

ВРАЩАТЕЛЬНАЯ ПАРА – одноподвижная пара, допускающая вращательное движение одного звена относительно другого [см. кинематическая пара].

ПОСТУПАТЕЛЬНАЯ ПАРА – одноподвижная пара, допускающая прямолинейно-поступательное движение одного звена относительно другого.

ПЛОСКИЙ МЕХАНИЗМ – механизм, точки звеньев которого описывают траектории, лежащие в параллельных плоскостях.

ПРОСТРАНСТВЕННЫЙ МЕХАНИЗМ – механизм, точки звеньев которого описывают пространственные траектории или траектории, лежащие в пересекающихся плоскостях.

ШАРНИРНЫЙ МЕХАНИЗМ – механизм, звенья которого образуют только вращательные пары. Примерами шарнирных механизмов являются кривошипно-коромысловый механизм, двухкоромысловый механизм и др.

ШАРНИРНЫЙ ЧЕТЫРЕХЗВЕННЫЙ МЕХАНИЗМ (шарнирный четырехзвенник) – шарнирный механизм, содержащий три подвижных звена и стойку.

РЫЧАЖНЫЙ МЕХАНИЗМ – механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары. Примерами рычажного механизма являются кривошипно-ползунный механизм, кулисный механизм и др.

КРИВОШИПНО-КОРОМЫСЛОВЫЙ МЕХАНИЗМ – шарнирный четырехзвенный механизм, в состав которого входят кривошип и коромысло.

КРИВОШИПНО-ПОЛЗУННЫЙ МЕХАНИЗМ – рычажный четырехзвенный механизм, в состав которого входят кривошип и ползун. Кривошипно-ползунный механизм служит для преобразования вращательного движения кривошипа в возвратно-поступательное движение ползуна или, наоборот, возвратно-поступательного движения ползуна во вращательное движение кривошипа.

КРИВОШИПНО-КУЛИСНЫЙ МЕХАНИЗМ – рычажный четырехзвенный механизм, в состав которого входят кривошип и кулиса. Кривошипно-кулисный механизм служит для передачи и преобразования вращательного движения кривошипа во вращательное или качательное движение кулисы и, наоборот, движение кулисы во вращение кривошипа.

СТОЙКА (редко: корпус, рама, станина, основание) – звено, принимаемое за неподвижное.

КРИВОШИП (иногда: коленчатый вал, коленвал, эксцентрик, водило) – вращающееся звено, которое может совершать полный оборот вокруг неподвижной оси.

КОРОМЫСЛО (редко рычаг) – вращающееся звено, которое может совершать только неполный оборот вокруг неподвижной оси.

ПОЛЗУН (поршень – в двигателях и компрессорах, толкатель – в кулачковых механизмах, суппорт – в станках, кулисный камень) – звено образующее поступательную пару с другим звеном (чаще всего со стойкой).

КУЛИСА – звено, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару.

ШАТУН – звено, образующее кинематические пары только с подвижными звеньями.

ШАТУННАЯ КРИВАЯ – траектория, описываемая какой-либо точкой шатуна.

ДВУХКРИВОШИПНЫЙ МЕХАНИЗМ – шарнирный четырехзвенный механизм, в который входят два кривошипа. Двухкривошипный механизм служит для передачи и преобразования вращательного движения. За один оборот одного кривошипа другой кривошип совершает также один оборот. Равномерному вращению одного кривошипа соответствует обычно неравномерное вращение другого кривошипа.

ДВУХКОРОМЫСЛОВЫЙ МЕХАНИЗМ – шарнирный четырехзвенный механизм, в состав которого входят два коромысла. Двухкоромысловый механизм служит для преобразования качательного движения одного коромысла в качательное движение другого коромысла.

ВХОДНОЕ ЗВЕНО – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Входное звено соединено с двигателем либо с выходным звеном другого механизма.

ВЫХОДНОЕ ЗВЕНО – звено, совершающее движение, для выполнения которого предназначен механизм. Выходное звено соединено с исполнительным устройством (рабочим органом, указателем прибора), либо со входным звеном другого механизма.

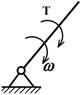
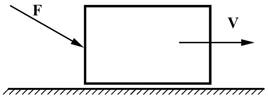
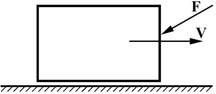
ВЕДУЩЕЕ ЗВЕНО – звено, для которого сумма элементарных работ внешних сил, приложенных к нему, положительна. Для вращающихся ведущих звеньев (схема а) момент Т и угловая скорость , а для поступательно движущегося ведущего звена проекция силы F на направление движения и линейная скорость V (схема б) направлены в одну сторону.

а)

б)

Обычно ведущее звено совпадает с входным звеном, но в процессе движения одно и то же входное звено может быть ведущим или ведомым. Например, поршень в двигателе внутреннего сгорания при сгорании смеси – ведущее звено, но при всасывании и сжатии смеси, а также при выпуске отработанных газов – ведомое звено.

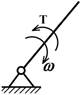
ВЕДОМОЕ ЗВЕНО – звено, для которого сумма элементарных работ внешних сил, приложенных к нему, отрицательна. Для вращающегося ведомого звена (схема а) момент силы Т и угловая скорость ω, а для поступательно движущегося звена (схема б) проекция силы F на направление движения ведомого звена и линейная скорость V направлены в противоположные стороны.

а)

б)

Обычно ведомое звено совпадает с выходным звеном, но в процессе движения одно и то же выходное звено может быть ведомым или ведущим, например, колесо электровоза при разгоне – ведомое звено, а при замедлении на ровном участке – ведущее звено (двигатель, соединенный с колесом через редуктор превращается в генератор и отдает энергию в сеть).

СТЕПЕНЬ ПОДВИЖНОСТИ МЕХАНИЗМА – целое число (W), показывающее сколько независимых движений нужно подвести к механизму, чтобы на выходе получить одно или наоборот. Большинство механизмов имеет степень подвижности W = 1; у дифференциальных механизмов W = 2; у роботов и манипуляторов W = 4 – 8 (чаще всего у них W = 4), также как и у основного механизма экскаватора.

СИНТЕЗ МЕХАНИЗМОВ – проектирование схемы механизма по заданным его свойствам. Синтез включает в себя выбор структурной схемы и определение постоянных параметров выбранной схемы механизма по заданным его свойствам. Различают: структурный синтез механизмов – выбор его схемы; метрический синтез – нахождение размеров звеньев и динамический синтез – распределение масс звеньев.

СИНТЕЗ МЕХАНИЗМОВ ПО ЧЕБЫШЕВУ – синтез механизмов по методу наилучшего равномерного приближения функций.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Строительная механика

00:00:00