Лабораторные работы

Главная

Лабораторная работа №30

Динамическая балансировка ротора

Цель работы: знакомство с методами уравновешивания вращающихся деталей и узлов, процессом динамической балансировки ротора.

Вращательное движение звеньев является в современной технике одним из доминирующих. При таком движении, как известно, всегда имеют место силы инерции, так как вращение звена обязательно происходит с ускорением.

Ускорение во вращательном движении раскладывается в общем случае на нормальную и касательную составляющие. Соответственно и сила инерции, равная произведению массы звена на ускорение его центра масс, может быть разложена на составляющие силы - нормальную и касательную.

Опасной силой инерции при вращении звена является НОРМАЛЬНАЯ СИЛА. Если эта сила еще и не уравновешена, то ее вредное действие возрастает: кроме разрыва тела вращения, который может произойти при достижении этим телом определенной критической скорости, неуравновешенная сила инерции приводит к возникновению в опорных подшипниках звена добавочных динамических реакций. Неуравновешенная нормальная сила инерции не постоянна по направлению - она вращается вместе со звеном, вызывая раскачивание опор и нарушение в них режима трения. Неуравновешенные нормальные силы инерции вызывают шум, вибрации, а в момент резонанса могут привести к поломке машины.

Нормальные силы инерции точечных масс, распределенных по звену, приводятся:

1. К нулю.

2. К силе (главному вектору).

3. К паре (главному моменту).

4. К силе и паре (винту).

Если силы инерции приводятся к нулю, то звено уравновешено; к силе - не уравновешено статически; к паре - звено не уравновешено динамически; к силе и паре - смешанный случай неуравновешенности звена.

Схематично перечисленные случаи неуравновешенности показаны на рис. 1.

Процесс выявления и устранения неуравновешенности звена называется б а л а н с и р о в к о й звена. В зависимости от вида неуравновешенности балансировка подразделяется на с т а т и ч е с к у ю и д и н а м и ч е с к у ю. При этом под динамической балансировкой понимают устранение как динамической (рис. 1, б), так и смешанной (рис. 1, в) неуравновешенности звена.

Целью динамической балансировки является:

1. Выявление величины и плоскости действия момента неуравновешенных сил инерции звена.

Устранение влияния этого момента путем изменения массы звена.

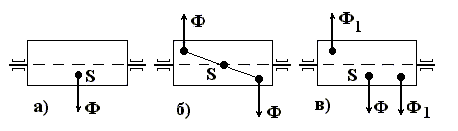
Рис. 1. Виды неуравновешенности:
а) статическая; б) динамическая; в) смешанный случай;
S - центр масс звена; Ф1,Ф - силы инерции

Звенья, имеющие форму тел вращения, проектируются уравновешенными. Однако при их изготовлении вносятся погрешности, которые могут привести к неуравновешенности звена - к несовпадению главной центральной оси инерции с осью вращения звена (главная центральная ось инерции проходит через центр масс звена; нормальных сил инерции относительно этой оси и любой другой, ей перпендикулярной, равен нулю).

На рис. 2 изображено звено в форме круглого диска.

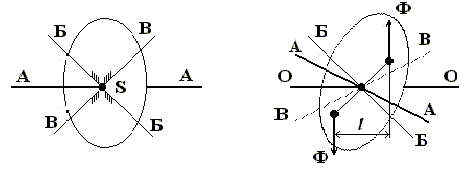
Рис. 2,3. Звено в виде круглого диска и звено
с осью вращения, являющейся центральной осью инерции

АА, ББ, ВВ - главные центральные оси инерции (S - центр масс звена). Оси ББ и ВВ лежат в плоскости диска, ось АА - ей перпендикулярна.

При вращении диска вокруг любой из этих осей не будет возникать никаких моментов от нормальных сил инерции, или иначе - диск будет полностью уравновешен.

На рис. 3 показан случай, когда ось О-О вращения диска является центральной осью инерции (проходит через центр масс), но не главной. Нормальные силы инерции точечных масс диска приводятся в этом случае к паре (главному моменту):

M=Фl.

Главный вектор сил инерции равен нулю. В итоге диск оказывается неуравновешенным динамически (схема на рис. 1, б).

В связи с тем, что центр масс S диска находится на оси вращения, обнаружить динамическую неуравновешенность можно только при достаточно быстром вращении диска, когда становится заметным действие момента неуравновешенных сил инерции. Устранение динамической неуравновешенности диска заключается в совмещении главной центральной оси инерции АА с осью вращения ОО.

На рис. 4 изображен вал с двумя неуравновешенными массами m, расположенными в одной осевой плоскости на одинаковом расстоянии от оси вращения О-О. Развиваемые неуравновешенными массами m силы инерции образуют пару с моментом M=Фl, действующим в осевой плоскости вала. Вал неуравновешен динамически, но уравновешен статически (центр масс S лежит на оси вращения).

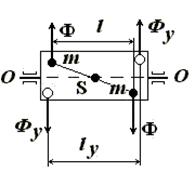
Рис. 4. Вал с двумя неуравновешенными массами

Уравновешивание вала достигается из условия равенства моментов сил инерции:

Противовесы следует устанавливать в плоскости расположения неуравновешенных масс m.

Динамическую неуравновешенность вала (как и диска, рис. 3) также можно обнаружить только при его вращении, когда опять-таки проявляется действие в осевой плоскости вала момента неуравновешенных сил инерции.

Рассмотрим теперь случай смешанной неуравновешенности вала и его балансировку (схема на рис. 1, в).

Пусть имеются две неуравновешенные неодинаковые по величине массы m₁ и m₂, расположенные в разных плоскостях, как вращения, так и осевых (рис. 5, а).

Нормальные силы инерции, развиваемые этими массами, обозначим соответственно P, Q (рис. 5,б).

Для уравновешивания указанных сил инерции проведем через точки К₁ и К₂ перпендикулярно оси вращения две плоскости пл. I и пл. II. Эти плоскости называются плоскостями уравновешивания (точки К₁ и К₂ на оси вращения ОО выбраны произвольно).

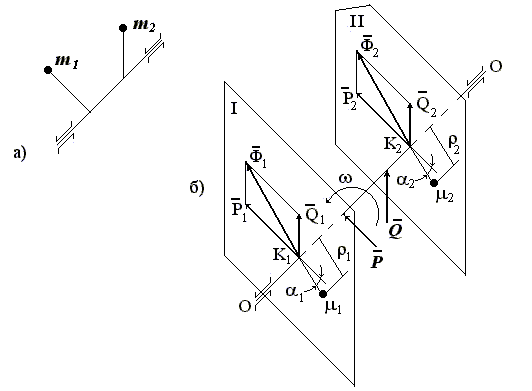
Рис. 5. Схема вала с двумя неуравновешенными массами:

а) схема смешанной неуравновешенности; б) расчетная схема

Разложим силы инерции P и Q на параллельные составляющие Р₁ и Р₂, Q₁ и Q₂, лежащие в плоскостях уравновешивания и приложенные попарно в точках К₁ и К₂. Заменим составляющие P₁ и Q₁ их равнодействующей Ф₁, а составляющие P₂ и Q₂ - равнодействующей Ф₂.

Силу инерции Ф₁, действующую в плоскости уравновешивания 1, можно уравновесить противовесом массы с центром масс на радиусе (вектор противоположен по направлению вектору ) исходя при этом из условия:

Аналогично уравновешивается и сила инерции Ф₂ (получена от сложения P₂ и Q₂) в плоскости уравновешивания II:

Таким образом, добавочные грузы (противовесы), массы которых равны и , расположенные в двух произвольно выбранных плоскостях уравновешивания, полностью уравновешивают данную систему сил.

Плоскости уравновешивания выбираются из соображений удобства или конструктивно.

Величину уравновешивающей силы инерции в каждой из плоскостей уравновешивания можно представить в виде:

Скалярное произведение

где i =1,2 , носит название статического момента уравновешивающей массы или дисбаланса звена.

Положение линии действия уравновешивающей силы инерции (положение плоскости дисбаланса) определяется углом , отсчитываемым от некоторой прямой в плоскости уравновешивания (рис. 5,б; i =1,2).

Следует заметить, что дисбаланс не зависит от скорости вращения звена.

В последнем примере неуравновешенности вала при расположении неуравновешенных масс по рис. 5, а, имеет место две плоскости дисбаланса. Положение этих плоскостей определяется углами и , отсчет которых ведется от некоторой осевой плоскости вала.

П Р А К Т И Ч Е С К А Я Ч А С Т Ь

На рис. 6 изображена схема станка, предложенного Б.В.Шитиковым для динамической балансировки роторов.

Рама (1) может колебаться вокруг горизонтальной оси О, перпендикулярной оси вращения ротора. Амплитуда А колебаний рамы определяется с помощью максимального (не сбрасывает показаний) индикатора (2). Разгон ротора производится электромотором (3) при нажатии на рукоятку (4). Восстанавливающий момент при колебаниях рамы обеспечивается торсионной пружиной (5). В подшипниках (6) установлен уравновешивающий ротор (7). На валу ротора закреплены два диска (8) и (9) с прорезями для установки уравновешивающих масс. Эти диски моделируют плоскости уравновешивания - I и II .

Плоскость уравновешивания II (диск 9) выбрана так, что в ней располагается ось О колебаний рамы 1. Неуравновешенная сила инерции Ф₂ , лежащая в этой плоскости не дает момента относительно оси О.

Момент относительно оси О создает только неуравновешенная сила инерции Ф₁, лежащая в плоскости уравновешивания (I-I) (диск 8). Момент этой силы равен:

где - скорость вращения ротора, t - время.

Этот момент вызывает вынужденные колебания рамы (1) вокруг оси О.

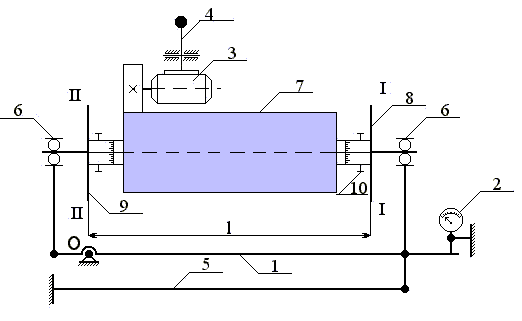
Рис. 6. Схема станка для динамической балансировки ротора:
1- рама; 2 - индикатор; 3 - электромотор; 4 - рукоятка; 5 - торсионная пружина; 6 - подшипник;

7 - уравновешиваемый ротор; 8,9 - диски для установки уравновешивающих масс;

10 - винт фиксации угловой координаты

Неуравновешенность в плоскости (I-I) (диск 8) представим как статический момент неуравновешенной массы :

Задача состоит в определении численного значения, направления и плоскости действия этого статического момента.

Последовательность выполнения работы

1. По уровню проверьте горизонтальность установки рамы (1).

2. Совместите риску диска (8) с нулевым делением нониуса.

3. Электромотором (3) разгоните ротор (7) за резонансные обороты. Отключите электромотор.

4. Измерьте индикатором (2) резонансную амплитуду А₁ при выбеге ротора (рис. 7). Колебания рамы 1 с амплитудой А₁ вызваны имеющим место дисбалансом , который назовем исходным дисбалансом или исходной неуравновешенностью.

5. В любую прорезь диска 8 установите один из грузов массы в наборе грузы 10, 20 и 30 г) на выбранном расстоянии от оси вращения (рис. 8).

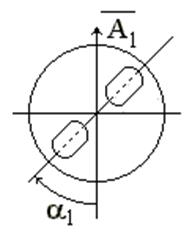
Рис. 7. Резонансная амплитуда при выбеге ротора
при отсутствии добавочной массы

6. Повторите операции 3 и 4. Измерьте резонансную амплитуду А₂. Амплитуда А₂ может быть представлена как геометрическая сумма амплитуд А₁ и а (рис. 9):

где а - амплитуда колебаний от установленного груза с массой .

7. Груз с массой переставьте в противоположную прорезь с тем же расстоянием от оси вращения (рис. 10).

8. Повторите операции 3 и 4, измерьте резонансную амплитуду А₃. Амплитуда А₃ представляется как геометрическая сумма амплитуд А₁ и а (рис. 11):

ВНИМАНИЕ! Запомните прорезь, в которой был установлен груз с массой при измерении амплитуды А₃. Если теперь параллелограммы амплитуд (рис. 9 и 11) сблизить до совпадения отмеченных черточками сторон, то получится треугольник со сторонами 2А₁, А₂ , А₃ (рис. 12). Из треугольника амплитуд определяем значения величин для уравновешивания статического момента (исходного дисбаланса) в плоскости уравновешивания 1 (диск 8).

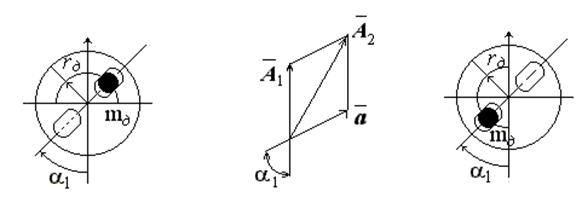
Рис. 8,9,10. Установка массы в первую прорезь,
векторное определение амплитуды, установка
массы во вторую прорезь

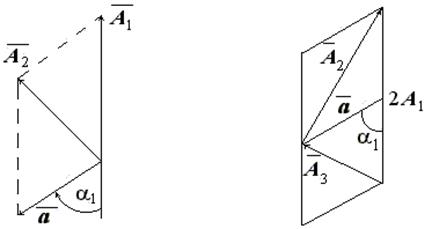
Рис. 11,12. Сложение амплитуд, треугольник амплитуд

9. Постройте треугольник амплитуд со сторонами 2А₁, А₂ , А₃ в крупном масштабе (М 100: 1, рис. 13).

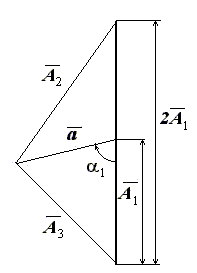
Рис. 13. Треугольник амплитуд для определения статического момента

Каждая амплитуда определяется не менее трех раз. Треугольник амплитуд строится по их средним значениям.

ВНИМАНИЕ! Расчетным является треугольник амплитуд, построенный на рис.13 (строится только этот треугольник).

Построив затем медиану стороны 2А₁, найдем в масштабе треугольника амплитуду (-А₁) для уравновешивания исходного дисбаланса

и положение осевой плоскости его действия (угол ).

10. Определите статический момент для уравновешивания исходного дисбаланса:

В соотношении А₁ и а - натуральные (не в масштабе) значения амплитуд. Длину отрезка, изображающего амплитуду а, найти из треугольника амплитуд (рис. 13) измерением. Затем умножением на масштаб треугольника перейдите от отрезка к натуре.

Исходная неуравновешенность и уравновешивающий статический момент

равны численно, но направлены противоположно.

11. Возьмите допустимую величину уравновешивания массы (10, 20 или 30 г.) и из предыдущего соотношения найдите значение радиуса установки этой массы:

12. Измерьте угол между медианой а и амплитудой (-А₁) рис. 13.

Угол определяет положение плоскости дисбаланса , т.е. осевой плоскости ротора, в которой должна располагаться уравновешивающая масса .

13. Установите уравновешивающую массу на радиусе (определен в п. 11) в той же прорези, в которой был установлен дополнительный груз с массой при измерении амплитуды А₃.

14. Поверните диск 8 на угол и закрепите стопорным винтом 10. Направление поворота найдите попытками.

ПРИМЕЧАНИЕ. Можно измерить угол ), но тогда уравновешивающую массу следует устанавливать в ту прорезь, в которой дополнительный груз с массой при изменении амплитуды А₂.

15. Контрольные разгоны. Наибольшая амплитуда после уравновешивания не должна превышать 0,05 мм.

Допустимая неуравновешенность (дисбаланс) определяется техническими условиями. При этом задается величина статического момента или амплитуды колебаний.

16. Составьте отчет по прилагаемой форме.

ПРИМЕЧАНИЕ.

1. Численное значение и положение плоскости действия исходной неуравновешенности можно определить аналитически по формулам:

Для уравновешивания дисбаланса в плоскости II (плоскость действия силы инерции Ф₂) вал необходимо развернуть, установив его так, чтобы плоскость диска 8 прошла через ось О качания рамы, и повторить процесс уравновешивания в плоскости уравновешивания II (диск 9).

Контрольные вопросы

- Причины и последствия неуравновешенности звеньев.

- Почему необходимо уравновешивать силы инерции в роторах?

- Виды неуравновешенностей.

- Динамическая неуравновешенность и ее проявление.

- Динамическая балансировка и ее цель.

- Принцип работы балансировочного станка Б.В.Шитикова.

- Порядок выполнения работы по уравновешиванию звена.

Форма отчета

1. Схема установки (по рис. 6)

ПАРАМЕТРЫ ЗАДАВАЕМОГО ДИСБАЛАНСА

2. Масса дополнительного груза - = , (г).