Главная
Кинематический синтез и анализ сложных
зубчатых механизмов
Задание.
1.1. Установить структуру механизма и определить его
тип.
1.2. Вывести формулу передаточного отношения механизма,
выразив его через числа зубьев колес.
1.3. Подобрать числа зубьев всех колес, обеспечивая
заданные условия синтеза механизма (общее передаточное отношение iAB механизма, количество сателлитов у планетарной
ступени и т.д.); если количество сателлитов не оговорено, принять любое nw>1, удовлетворяющее условиям соседства и сборки.
Передаточные отношения механизма или отдельных
ступеней задает консультант.
По подобранным числам зубьев колес рассчитать
фактическое передаточное отношение механизма ![]() и сравнить по
модулю с тем, которое соответствует условиям синтеза (допустимая погрешность
и сравнить по
модулю с тем, которое соответствует условиям синтеза (допустимая погрешность ![]() ).
).
1.4. Считая угловую скорость ωB выходного вала B зубчатого механизма
заданной и равной по модулю угловой скорости входного звена рычажного механизма
в задаче 2, определить абсолютные угловые скорости всех звеньев; для звеньев,
образующих вращательные кинематические пары, рассчитать относительные угловые
скорости.
1.5. На листе формата А4 вычертить (желательно в масштабе 1:1) схему
механизма в двух проекциях; на одной из проекций показать расположение
сателлитов или связанных колес с учетом количества потоков. При определении
диаметров колес принять их модуль m =
Пример. Произвести синтез и кинематический анализ
механизма, схема которого приведена на рис. 1. Подбором чисел зубьев обеспечить
получение передаточного отношения iAB =-15,2. Угловая скорость выходного вала |ωB|=6,5 с-1.
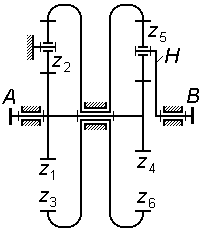
Рис.1
Решение. Зубчатые
колеса z4,
z5, z6 и водило H составляют дифференциальную ступень, у которой угловые
скорости колес z4 и z6 связаны соосной рядовой кинематической цепью, образуемой
колесами z1, z2 и z3. Таким образом, механизм является замкнутым
дифференциалом. Его кинематику можно описать следующими соотношениями:
- для
дифференциальной ступени
![]()
- для замыкающей цепи
![]()
- уравнения кинематических связей
![]()
Учитывая эти равенства и то, что ![]() , можно записать
, можно записать

отсюда получаем формулу передаточного отношения
механизма

Можно задать значение дроби z6/z4 и
рассчитать величину z3/z1, при которой будет обеспечено требуемое передаточное
отношение iAB:

Пусть, например, ![]() ; тогда для отношения z3/z1 получим
требуемое значение
; тогда для отношения z3/z1 получим
требуемое значение

которое можно довольно точно представить подходящей
обыкновенной дробью
![]()
Проверим точность подбора чисел зубьев по величине
фактического передаточного отношения:

отклонение полученной величины от
заданной составляет
![]()
что вполне допустимо.
Числа зубьев связанных колес z2 и
сателлитов z5 найдем из условий соосности:
![]()
откуда
![]()
![]()
Примем z2=14
и z5=15.
Из условий соседства найдем предельно допустимые
значения числа связанных колес ![]() и сателлитов
и сателлитов ![]() :
:


Из условия сборки для замыкающей кинематической цепи z1, z2, z3
![]()
следует, что в качестве ![]() пригодно
значение любого делителя числа 75, не превышающее 7 (здесь Ц2
- произвольное целое число); примем
пригодно
значение любого делителя числа 75, не превышающее 7 (здесь Ц2
- произвольное целое число); примем ![]() =5.
=5.
Аналогично, для дифференциальной ступени z4, z5, z6 должна
быть целой величина
![]()
и поэтому можно принять число сателлитов ![]() =3 (это единственный делитель числа 69, отличный от 1
и меньший 6).
=3 (это единственный делитель числа 69, отличный от 1
и меньший 6).
Таким образом, для колес редуктора подобраны следующие
числа зубьев и потоков мощности: z1=24; z2=14; z3=51; ![]() =5;
=5;
z4=19; z5=15; z6=50; ![]() =3.
=3.
Рассчитаем кинематику механизма.
Полагая ![]() и ωB= -6,5 c-1 (знаки iAB и ωB
должны совпадать), найдем угловую скорость входного вала и расположенных на нем
зубчатых колес
и ωB= -6,5 c-1 (знаки iAB и ωB
должны совпадать), найдем угловую скорость входного вала и расположенных на нем
зубчатых колес
![]()
угловая скорость связанных колес z2
![]()
угловая скорость колес z3 и z6
![]()
![]()
учитывая, что ωH=ωB= -6,5 c-1, найдем угловую скорость сателлитов z5
![]()
Найдем относительные угловые скорости во вращательных
парах:
![]()
![]()
Для вычерчивания кинематической схемы механизма
необходимо принять значения межосевых расстояний рядовой и планетарной частей:

для каждой части механизма разрешается принять любое
из двух возможных значений, если они неодинаковы.
Примем: для
рядовой части
![]()
для планетарной –
![]()
Диаметры начальных окружностей: для рядовой цепи
![]()
![]()
![]()
![]()
для планетарной ступени
![]()
![]()
![]()
![]()
Сателлиты z5 и связанные колеса z2 имеют по
две начальных окружности - во внешнем и внутреннем зацеплении.
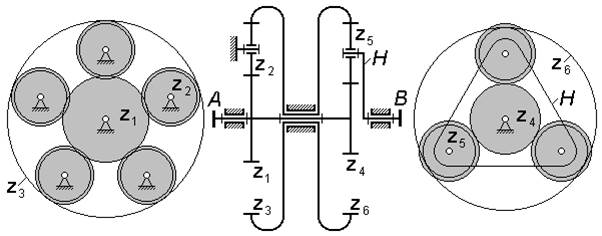
Рис.2
На рис.2
показан пример оформления
графической части задачи.
Варианты заданий
|
Вариант 01 |
Вариант 02 |
|
Вариант 03 |
Вариант 04 |
|
Вариант 05 |
Вариант 06 |
|
Вариант 07 |
Вариант 08 |
|
Вариант 09 |
Вариант 10 |
|
Вариант 11 |
Вариант 12 |
|
Вариант 13 |
Вариант 14 |
|
Вариант 15 |
Вариант 16 |
|
Вариант 17 |
Вариант 18 |
|
Вариант 19 |
Вариант 20 |
|
Вариант 21 |
Вариант 22 |
|
Вариант 23 |
Вариант 24 |
|
Вариант 25 |
Вариант 26 |
|
Вариант 27 |
Вариант 28 |
|
Вариант 29 |
Вариант 30 |
|
Вариант 31 |
Вариант 32 |
|
Вариант 33 |
Вариант 34 |
|
Вариант 35 |
Вариант 36 |
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Строительная механика