Главная
Структурное
исследование плоских рычажных механизмов
Задание. Проанализировать структуру
механизмов заданной схемы.
1.1. Вычертить
схему механизма.
1.2. Пронумеровать звенья арабскими цифрами, присвоив
последний номер неподвижному звену (стойке).
Установить класс каждой кинематической пары,
образуемой звеньями механизма.
1.3. Рассчитать
степень подвижности механизма и проанализировать полученный результат. Если в
механизме присутствуют пассивные связи и (или) местные подвижности, избавиться
от них и повторить расчет.
1.4. Заменить
высшие пары (если они имеются в механизме) кинематическими цепями с низшими
парами; замену произвести непосредственно на кинематической схеме, для
обозначения фиктивных звеньев в заменяющем механизме использовать обозначения ![]() ,
, ![]() и т.д.
и т.д.
Определить степень подвижности заменяющего механизма,
результат сопоставить с полученным
в п. 1.3.
1.5. Для заменяющего механизма вычертить структурную
схему (если это требуется для облегчения структурного анализа); установить
возможные варианты выбора начальных звеньев и для каждого варианта написать формулу
строения механизма.
Для каждой формулы строения указать класс, вид и
порядок структурных групп, а также класс механизма.
Пример. Произвести структурное исследование механизма по
приведенной схеме.

Рис.1
Решение. Степень подвижности механизма
![]() ;
;
здесь n = 6
- число подвижных звеньев;
![]() - число пар четвертого
класса (высших пар);
- число пар четвертого
класса (высших пар);
![]() - число пар пятого
класса (из них - 1 поступательная пара и 6 вращательных, при этом шарнир O - двойной); таким образом,
- число пар пятого
класса (из них - 1 поступательная пара и 6 вращательных, при этом шарнир O - двойной); таким образом,
![]() .
.

Рис. 2
Механизм содержит местную подвижность, не влияющую на
его кинематику – вращение ролика 3 относительно шатуна 4. Устраним эту
подвижность, объединив ролик и шатун в одно звено (рис. 2) и вновь рассчитаем
число степеней свободы механизма
![]() .
.
Этот результат в отличие от предыдущего показывает
истинную (фактическую) подвижность механизма; таким образом, его положение
полностью характеризуется одной обобщенной координатой, или, что то же самое,
заданием положения одного любого звена, образующего кинематическую пару со
стойкой.

Рис.3
Произведем замену каждой высшей кинематической пары
двумя парами пятого класса и фиктивным звеном; на рис. 3 изображена процедура
замены, причем точки B, С1 и С2 - центры кривизны профилей, участвующих в высших парах.
В результате замены
высших пар получаем мгновенно - заменяющий механизм (рис. 4) с той же
подвижностью, что и до замены; поскольку
![]() ,
, ![]() ,
, ![]() , то, следовательно
, то, следовательно
![]() .
.

Рис.4
С целью облегчения структурного анализа можно для
заменяющего механизма построить так называемую структурную схему, при
изображении которой используют следующие условности:
- все кинематические пары пятого класса (и
вращательные, и поступательные) изображают как вращательные;
- звенья, участвующие в нескольких кинематических
парах, изображают в виде соответствующих многоугольников.
Структурная схема для исследуемого механизма изображена на рис. 5
(символом П на ней помечены те вращательные пары, которые в реальной и
мгновенно заменяющей схемах являются поступательными).

Рис.5
Очевидно, что исследуемый механизм может иметь только
одно начальное звено из множества – 1, 2, 5, или 6.
Запишем соответствующие варианты формул строения
механизма:
![]()
![]()
![]()
![]()
в этих формулах:
[1, 7], [2, 7], [5, 7] и [6, 7] – начальные механизмы I класса, соответствующие выбранным начальным звеньям;
(2, 4, 5, ![]() ) и (2, 4, 5,
) и (2, 4, 5, ![]() ) – группы III класса 3-го
порядка;
) – группы III класса 3-го
порядка;
все остальные группы являются группами II класса: (1, ![]() ) и (2, 4) - 1-го вида, (4, 5) - 2-го вида, и (6,
) и (2, 4) - 1-го вида, (4, 5) - 2-го вида, и (6, ![]() ) - 3-го вида.
) - 3-го вида.
Таким образом, при начальных звеньях 2 и 5 механизм
относится к II классу, а при начальных звеньях
1 и 6 – III классу.
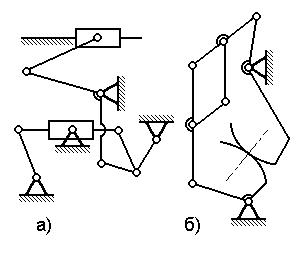
Варианты заданий
|
Вариант 01 |
Вариант 02 |
|
|
Вариант 03 |
Вариант 04 |
|
|
Вариант 05 |
Вариант 06 |
|
|
Вариант 07 |
Вариант 08 |
|
|
Вариант 09 |
Вариант 10 |
|
|
Вариант 11 |
Вариант 12 |
|
|
Вариант 13 |
Вариант 14 |
|
|
Вариант 15 |
Вариант 16 |
|
|
Вариант 17 |
Вариант 18 |
|
|
Вариант 19 |
Вариант 20 |
|
|
Вариант 21 |
Вариант 22 |
|
|
Вариант 23 |
Вариант 24 |
|
|
Вариант 25 |
Вариант 26 |
|
|
Вариант 27 |
Вариант 28 |
|
|
Вариант 29 |
Вариант 30 |
|
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Строительная механика