Главная
Лабораторная работа №8
Кинематический
анализ механизмов по моделям
Цель работы: определение кинематических характеристик механизмов
методом построения планов скоростей и ускорений.
Задачей
кинематического анализа является определение линейных скоростей и ускорений
точек звеньев и угловых скоростей и ускорении всех звеньев графо–аналитическим
методом, т.е. методом построения планов скоростей и ускорений.
Планы скоростей
и ускорений имеют следующие свойства:
1) В полюсе плана скоростей (ускорений) линейные
скорости (ускорения) равны нулю.
2) Лучи, проведенные из полюса плана скоростей
(ускорений) до соответствующих точек, обозначают абсолютные линейные скорости (ускорения)
аналогичных точек звеньев механизмов в выбранном масштабе.
3) Отрезки, соединяющие концы лучей, соответствуют
относительным скоростям (ускорениям) соответствующих точек звеньев в принятом
масштабе.
4) Отрезки прямых, соединяющих точки на схеме механизма,
и отрезки прямых, соединяющих концы векторов скоростей (ускорений) этих точек,
образуют подобные сходственно расположенные фигуры.
5) Направление угловых скоростей (ускорений)
определяются направлением возможности поворота звена на схеме механизма
вектором относительной скорости (ускорения) плана скоростей (ускорений),
приложенным к соответствующей точке звена механизма.
6) Концы векторов абсолютных скоростей (ускорений) на
планах скоростей (ускорений) обозначаются теми же буквами латинского алфавита
(но строчными), что и соответствующие точки на плане механизма. Например, для
механизма, изображенного на рисунке 1 на плане скоростей вектор ab соответствует звену плана механизма AВ и обозначает относительную скорость
точки В
относительно точки А звена АВ.
Рассмотрим пример построения планов скоростей и
ускорений для механизма, представленного на рисунке 1. План механизма построен
в масштабе, причем масштабный коэффициент длины равен
![]()
где lAB –
истинная длина звена АВ, м;
(АВ) – длина отрезка АВ в мм, взятая из плана механизма;
![]() – масштабный коэффициент, м/мм–1.
– масштабный коэффициент, м/мм–1.
Угловая скорость ведущего звена постоянная, т.е. ![]() = const.
= const.
Последовательность кинематического анализа
определяется формулой строения механизма, полученной в результате структурного
анализа. Формула строения рассматриваемого механизма
![]()
Кинематический анализ необходимо начинать с ведущего
звена со стойкой (механизма I класса), затем
переходить к кинематическому анализу групп Ассура второго класса первого вида II1 (2, 3),
состоящей из 2 и 3 звеньев.
Для построения плана скоростей (ускорений) необходимо
графически решить векторные уравнения:
1) Рассмотрим механизм первого класса I (О,
1), запишем векторное уравнение для определения скорости точки В звена 1, т.е.
![]() ,
,
где![]() -вектор скорости точки А, скорость точки А
равна 0;
-вектор скорости точки А, скорость точки А
равна 0;
![]() – вектор относительной скорости точки В1 относительно точки А, причем
– вектор относительной скорости точки В1 относительно точки А, причем ![]() , направлена по перпендикуляру к (АВ) в сторону
, направлена по перпендикуляру к (АВ) в сторону ![]() . Все это удобно записать так:
. Все это удобно записать так:
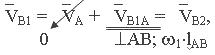 ,
,
так как скорость точки В1 и точки В2,
входящих во вращательную пару В,
равны.
2) Выбираем полюс плана скоростей (точка рV), решаем векторное уравнение графически. Так как
скорость точки А, принадлежащей
стойке О, равна нулю, то точка А звена 1 будет находиться в полюсе
плана скоростей и будет обозначена буквой (а). Из полюса (рV) откладываем вектор
![]() , изображающий на плане скоростей вектор скорости
, изображающий на плане скоростей вектор скорости ![]() , он перпендикулярен звену
АВ и направлен в сторону вращения
, он перпендикулярен звену
АВ и направлен в сторону вращения ![]() . Выбрав длину отрезка (рVb1),
определяем масштабный коэффициент плана скоростей:
. Выбрав длину отрезка (рVb1),
определяем масштабный коэффициент плана скоростей:
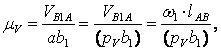 мс–1мм–1.
мс–1мм–1.
3) Рассмотрим группу Ассура II1 (2,3).
Определим скорость точки С, принадлежащая звену 2 и звену 3, которые образуют
кинематическую вращательную пару С, а поэтому
![]() .
.
Запишем два векторных уравнения и решим их графически:
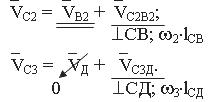
На плане скоростей из конца вектора (ab2) проводим направление вектора скорости`![]() перпендикулярно звену 2.
перпендикулярно звену 2.
Из полюса, где находится точка Д звена 3, так как`![]() равна нуля, проводим направление вектора
скорости`
равна нуля, проводим направление вектора
скорости`![]() перпендикулярно звену СД. Пересечения векторов`
перпендикулярно звену СД. Пересечения векторов`![]() и `
и `![]() даст на плане скоростей точку с2,3,
принадлежащую точке С
механизма. План скоростей представлен на рисунке 1.
даст на плане скоростей точку с2,3,
принадлежащую точке С
механизма. План скоростей представлен на рисунке 1.
4) Определим величину угловых ускорений звеньев 2 и 3.
Из векторных уравнений имеем:
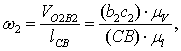 с–1;
с–1;
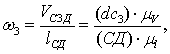 с–1;
с–1;
так как из плана скоростей ![]() ,
, ![]() ; а из плана механизма
; а из плана механизма ![]() .
.
5)
Определим направление угловых скоростей звеньев 2 и 3. Направление угловых
скоростей определяется по направлению векторов относительных скоростей
соответствующих точек звена. Например, направление ![]() определяется
направлением вектора (b2c2),
вектор (b2c2) из
плана скоростей условно переносим в точку
С звена СВ, если вектор (b2c2) поворачивает звено СВ вокруг точки В против часовой стрелки, то и направление угловой скорости
определяется
направлением вектора (b2c2),
вектор (b2c2) из
плана скоростей условно переносим в точку
С звена СВ, если вектор (b2c2) поворачивает звено СВ вокруг точки В против часовой стрелки, то и направление угловой скорости ![]() – против часовой
стрелки как это показано на рисунке 2.
– против часовой
стрелки как это показано на рисунке 2.
Рассмотрим построение плана ускорений.
Записываем и решаем векторные уравнения в той же
последовательности, что и при построении плана скоростей, т.е.
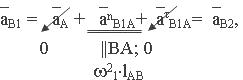
так как точки В1
и В2 образуют
вращательную пару В,
где аA –
ускорение точки А равно нулю, т.к.
точка А принадлежит стойке;
![]() – нормальное (центростремительное)
ускорение, направленное к «центру», т.е. к точке А, параллельно АВ;
– нормальное (центростремительное)
ускорение, направленное к «центру», т.е. к точке А, параллельно АВ;
![]() – тангенциальное
(касательное) ускорение равно нулю, т.к. по условию задачи
– тангенциальное
(касательное) ускорение равно нулю, т.к. по условию задачи ![]() , значит, равно нулю и угловое ускорение
, значит, равно нулю и угловое ускорение ![]() ведущего звена.
ведущего звена.
Выбираем полюс плана ускорений (точка ра).
Ускорение точки А равно нулю, значит,
точка А будет в полюсе плана
ускорений (точка а). Из полюса (ра) откладываем отрезок (аb1,2) = (pab1,2), изображающий на плане
ускорений вектор ускорения ![]() , он параллелен звену ВА
и направлен к центру вращения (точке А). Масштабный коэффициент равен
, он параллелен звену ВА
и направлен к центру вращения (точке А). Масштабный коэффициент равен ![]() , м×с–2мм–1.
, м×с–2мм–1.
6) Рассмотрим группу Ассура, запишем векторные
уравнения:
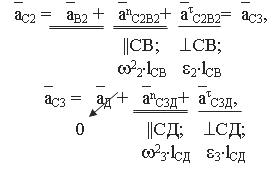
Из конца вектора (ab1,2) плана
ускорений проводим вектор (b2n2),
соответствующий в масштабе ![]() вектору нормального
ускорения аnС2В2 параллельно звену СВ в направлении к центру
вращения (точка В), из конца вектора (b2n2)
проводим перпендикулярно (b2n2) направление
вектора тангенциального ускорения
вектору нормального
ускорения аnС2В2 параллельно звену СВ в направлении к центру
вращения (точка В), из конца вектора (b2n2)
проводим перпендикулярно (b2n2) направление
вектора тангенциального ускорения ![]() , величина которого пока неизвестна. Из полюса проводим
параллельно звену СД в направлении к
центру вращения (точка Д) вектор центростремительного ускорения
, величина которого пока неизвестна. Из полюса проводим
параллельно звену СД в направлении к
центру вращения (точка Д) вектор центростремительного ускорения ![]() , величина которого известна, в масштабе
, величина которого известна, в масштабе ![]() ; затем из конца вектора (an3)
проводим перпендикуляр, соответствующий касательному ускорению
; затем из конца вектора (an3)
проводим перпендикуляр, соответствующий касательному ускорению ![]() . Линии векторов, соответствующих тангенциальным ускорениям
. Линии векторов, соответствующих тангенциальным ускорениям ![]() и
и ![]() пересекутся, на их
пересечении будет находится точка с2,3, соответствующая точке С на плане
механизма. Соединяем точку с2,3 с полюсом (ра) плана
ускорений.
пересекутся, на их
пересечении будет находится точка с2,3, соответствующая точке С на плане
механизма. Соединяем точку с2,3 с полюсом (ра) плана
ускорений.
7) Из
уравнений ускорений определяем величину угловых ускорений звеньев 2 и 3, т.е. ![]() и
и ![]() ;
;
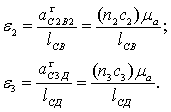
Определение направлений угловых ускорений ![]() и
и ![]() показано на рисунке 2.
показано на рисунке 2.
По плану скоростей можно найти скорость любой точки
механизма, например, ![]() .
.
Из плана ускорений можно найти величину полного,
тангенциального или центростремительного ускорения любой точки механизма,
например, ![]() .
.
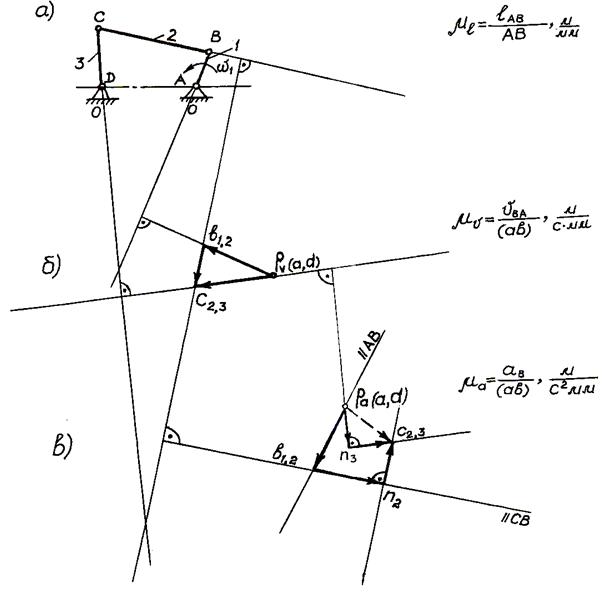
Рисунок 1 – План скоростей и ускорений
а) кинематическая схема механизма; б) план скоростей;
в) план ускорений
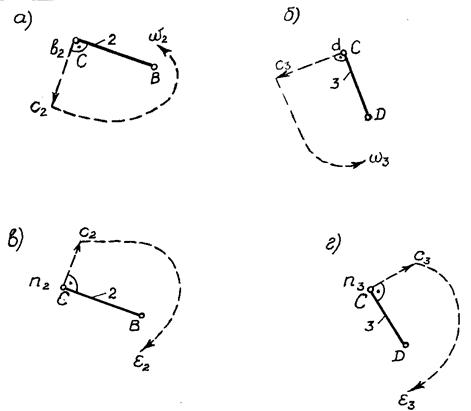
Рисунок 2 – Определение направлений угловых скоростей ![]() и угловых ускорений
и угловых ускорений ![]()
Порядок выполнения работы
1. Построить кинематическую схему механизма (план
механизма в масштабе![]() ) по модели, структурный анализ которого выполнен в
лабораторной работе №3. Написать формулу строения механизма.
) по модели, структурный анализ которого выполнен в
лабораторной работе №3. Написать формулу строения механизма.
2. Построить план скоростей в масштабе ![]() .
.
3. Определить по величине из плана скоростей скорости
всех точек механизма.
4. Определить величину и направление угловых скоростей
звеньев механизма.
5. Построить план ускорений в масштабе ![]() .
.
6. Определить полные ускорения всех точек механизма из
плана ускорений.
7. Определить величину и направление угловых ускорений
звеньев механизма.
Основные правила техники безопасности
1. Соблюдать осторожность при проведении лабораторной
работы, чтобы не вывести из строя модели механизмов.
Содержание отчета
1. Цель работы.
2. Тип, номер и наименование модели.
3. План механизма в масштабе.
4. План скоростей и план ускорений, построенные
в масштабе.
5. Определение величин скоростей точек механизма по
построенному плану скоростей.
6. Определение величин ускорений точек механизма по
плану ускорений.
7. Определение величин и направлений угловых скоростей
и ускорений звеньев механизма (с указанием направлений на звеньях механизма).
Контрольные вопросы
1. Что называется планом скоростей (ускорений)?
2. Чем определяется последовательность кинематического
анализа механизма?
3. Какими буквами латинского алфавита принято
обозначать точки на плане механизма, на планах скоростей и ускорений?
4. Как вычисляется масштабный коэффициент длины
(скорости, ускорения)?
5. Как по планам скоростей и ускорений найти величину
скоростей и ускорений точек механизма?
6.
Как по плану скоростей (ускорений) найти направление угловых скоростей (угловых
ускорений) звеньев механизма?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Строительная механика